Question

（1）已知α、β、γ都是銳角，且tanα=,tanβ=,tanγ=,試求α+β+γ的值.

（2）求arctan1+arctan2+arctan3的值.

Answer 1

思路分析：對于第（1）小題可先求出tan（α+β）的值，再把α+β視為一個整體，求出tan［（α+β）+γ］的值，最后用反正切函數表示出α+β+γ的值；對于第（2）小題，由于arctan1=π[]4,所以只需求出arctan2+arctan3的值即可.

解：（1）∵tanα=,tanβ=,∴.

又∵tanγ=,

∴.

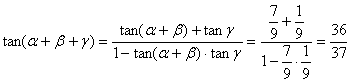∵α是銳角，且,∴0＜α＜.

同理，可得0＜β＜,0＜γ＜.

∴0＜α+β+γ＜.

∴α+β+γ=arctan.

（2）設arctan2=α,arctan3=β,

則tanα=2,tanβ=3且＜α＜,＜β＜.

∵,

又＜α+β＜π,∴α+β=,

即arctan2+arctan3=.

又arctan1=,∴arctan1+arctan2+arctan3=π.

方法歸納 已知三角函數值求角，需界定角的范圍，為準確地求出所求的角，可根據三角函數的單調性，把所求的角放置于兩個特殊角之間，以進一步縮小所求角的范圍，避免增根的出現.