在平面直角坐標系xOy中,已知圓C:x2+y2=r2和直線l:x=a(其中r和a均為常數,且0<r<a),M為l上一動點,A1,A2為圓C與x軸的兩個交點,直線MA1,MA2與圓C的另一個交點分別為P、Q.
(1)若r=2,M點的坐標為(4,2),求直線PQ方程;
(2)求證:直線PQ過定點,并求定點的坐標.
【答案】
分析:(1)通過r=2,M點的坐標為(4,2),求出A
1(-2,0),A
2(2,0).然后推出P、Q坐標,即可求直線PQ方程;
(2)證明法一:設A
1(-r,0),A
2(r,0).設M(a,t),求出直線MA
1的方程,直線MA
1的方程,通過直線與圓的方程聯立,求出直線PQ的方程,然后說明經過定點,求定點的坐標.
法二:設得A
1(-r,0),A
2(r,0).設M(a,t),求出直線MA
1的方程,與圓C的交點P設為P(x
1,y
1).求出直線MA
2的方程,與圓C的交點Q設為Q(x
2,y
2).點P(x
1,y
1),Q(x
2,y
2)在曲線[(a+r)y-t(x+r)][(a-r)y-t(x-r)]=0上,有P(x
1,y
1),Q(x
2,y
2)在圓C上,求出公共弦方程,說明經過定點,求定點的坐標.
解答:解:(1)當r=2,M(4,2),則A
1(-2,0),A
2(2,0).
直線MA
1的方程:x-3y+2=0,解
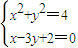
得

.…(2分)
直線MA
2的方程:x-y-2=0,解

得Q(0,-2). …(4分)
由兩點式,得直線PQ方程為:2x-y-2=0. …(6分)
(2)證法一:由題設得A
1(-r,0),A
2(r,0).設M(a,t),
直線MA
1的方程是:y=
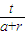
(x+r),
直線MA
1的方程是:y=
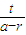
(x-r).…(8分)
解
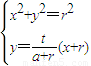
得

.…(10分)
解
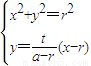
得
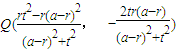
. …(12分)
于是直線PQ的斜率k
PQ=

,
直線PQ的方程為
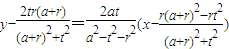
. …(14分)
上式中令y=0,得x=
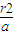
,是一個與t無關的常數.
故直線PQ過定點
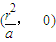
. …(16分)
證法二:由題設得A
1(-r,0),A
2(r,0).設M(a,t),
直線MA
1的方程是:y=
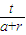
(x+r),與圓C的交點P設為P(x
1,y
1).
直線MA
2的方程是:y=
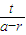
(x-r);與圓C的交點Q設為Q(x
2,y
2).
則點P(x
1,y
1),Q(x
2,y
2)在曲線[(a+r)y-t(x+r)][(a-r)y-t(x-r)]=0上,…(10分)
化簡得 (a
2-r
2)y
2-2ty(ax-r
2)+t
2(x
2-r
2)=0. ①
又有P(x
1,y
1),Q(x
2,y
2)在圓C上,圓C:x
2+y
2-r
2=0.②
①-t
2×②得 (a
2-r
2)y
2-2ty(ax-r
2)-t
2(x
2-r
2)-t
2( x
2+y
2-r
2)=0,
化簡得:(a
2-r
2)y-2t(ax-r
2)-t
2 y=0.
所以直線PQ的方程為(a
2-r
2)y-2t(ax-r
2)-t
2 y=0. ③…(14分)
在③中令y=0得 x=
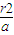
,故直線PQ過定點
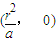
.…(16分)
點評:不考查直線與圓的位置關系,直線系方程的應用,考查計算能力與轉化思想.

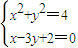 得
得 .…(2分)
.…(2分) 得Q(0,-2). …(4分)
得Q(0,-2). …(4分)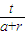 (x+r),
(x+r),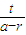 (x-r).…(8分)
(x-r).…(8分)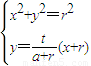 得
得 .…(10分)
.…(10分)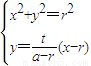 得
得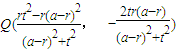 . …(12分)
. …(12分) ,
,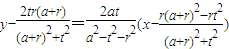 . …(14分)
. …(14分)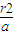 ,是一個與t無關的常數.
,是一個與t無關的常數.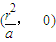 . …(16分)
. …(16分)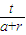 (x+r),與圓C的交點P設為P(x1,y1).
(x+r),與圓C的交點P設為P(x1,y1).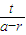 (x-r);與圓C的交點Q設為Q(x2,y2).
(x-r);與圓C的交點Q設為Q(x2,y2).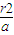 ,故直線PQ過定點
,故直線PQ過定點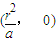 .…(16分)
.…(16分)

 如圖,在平面直角坐標系xOy中,銳角α和鈍角β的終邊分別與單位圓交于A,B兩點.若點A的橫坐標是
如圖,在平面直角坐標系xOy中,銳角α和鈍角β的終邊分別與單位圓交于A,B兩點.若點A的橫坐標是