B
分析:要求cosθ,就需要把條件里的sinθ轉化為cosθ消去,所以利用已知條件解出sinθ,兩邊平方再根據同角三角函數間的基本關系化簡可得到關于cosθ的一元二次方程,求出方程的解即可.
解答:由已知變形為2+2sinθ+2cosθ=1+sinθ-cosθ,解得sinθ=-1-3cosθ;
兩邊平方得:sin
2θ=1-cos
2θ=(-1-3cosθ)
2,
化簡得:5cos
2θ+3cosθ=0即cosθ(5cosθ+3)=0,
由題知cosθ≠0,所以5cosθ+3=0即cosθ=-

.
故選B
點評:此題考查學生靈活運用三角函數中的恒等變換,是一道基礎題.學生做題的思路是把正弦轉換為余弦.

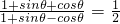 ,則cosθ的值等于
,則cosθ的值等于
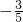
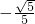

 .
.

 閱讀快車系列答案
閱讀快車系列答案