
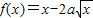 在(0,1)上為減函數.
在(0,1)上為減函數.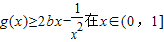 內恒成立,求b的取值范圍.
內恒成立,求b的取值范圍.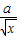 ,根據函數
,根據函數 在(0,1)上為減函數.得出f′(x)=1-
在(0,1)上為減函數.得出f′(x)=1- ≤0在(0,1)上恒成立,得到a的取值范圍,再利用導數研究函數的單調性得出f(x)的單調區(qū)間;
≤0在(0,1)上恒成立,得到a的取值范圍,再利用導數研究函數的單調性得出f(x)的單調區(qū)間;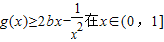 內恒成立,再分離出2b:2b≤x+
內恒成立,再分離出2b:2b≤x+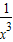 -
-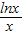 ,設h(x)=x+
,設h(x)=x+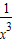 -
-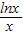 ,它在(0,1)上是減函數,只須2b小于h(1)即可求出b的取值范圍.
,它在(0,1)上是減函數,只須2b小于h(1)即可求出b的取值范圍.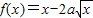 ,∴f′(x)=1-
,∴f′(x)=1-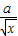 ,
,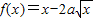 在(0,1)上為減函數.
在(0,1)上為減函數.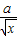 ≤0在(0,1)上恒成立,
≤0在(0,1)上恒成立,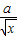 >0得:x>a2,
>0得:x>a2,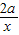 ≥0在(1,2)上恒成立,
≥0在(1,2)上恒成立,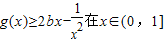 內恒成立,
內恒成立, ,
,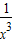 -
-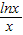 ,設h(x)=x+
,設h(x)=x+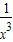 -
-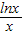 ,它在(0,1)上是減函數,
,它在(0,1)上是減函數,

 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源:2013年安徽省高考數學專項訓練:函數(解析版) 題型:選擇題
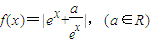 在區(qū)間[0,1]上單調遞增,則實數a的取值范圍是( )
在區(qū)間[0,1]上單調遞增,則實數a的取值范圍是( )查看答案和解析>>
科目:高中數學 來源:2012-2013學年遼寧省高三上學期第一次模擬考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
已知函數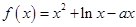 在(0,1)上是增函數.(1)求
在(0,1)上是增函數.(1)求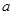 的取值范圍;
的取值范圍;
(2)設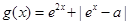 (
(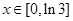 ),試求函數
),試求函數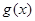 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三10月月考理科數學 題型:解答題
(本小題滿分14分)
已知函數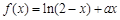 在(0,1)內是增函數.
在(0,1)內是增函數.
(1)求實數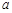 的取值范圍;
的取值范圍;
(2)若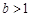 ,求證:
,求證: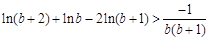 .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com