
已知函數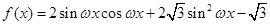 (
(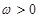 )的最小正周期為
)的最小正周期為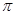 .
.
(Ⅰ)求函數 的單調增區間;
的單調增區間;
(Ⅱ)將函數 的圖象向左平移
的圖象向左平移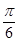 個單位,再向上平移
個單位,再向上平移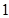 個單位,得到函數
個單位,得到函數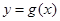 的圖象.求
的圖象.求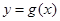 在區間
在區間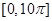 上零點的個數.
上零點的個數.
(Ⅰ)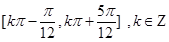 ;(Ⅱ)20.
;(Ⅱ)20.
解析試題分析:(Ⅰ)根據二倍角公式將原式化簡成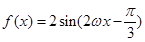 ,而周期
,而周期 ,則
,則 ,
,
從而得出 的解析式
的解析式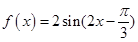 ,將
,將 當成一個整體,則有
當成一個整體,則有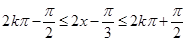 ,解得
,解得 ,故所以函數
,故所以函數 的單調增區間是
的單調增區間是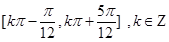 . (Ⅱ)將函數
. (Ⅱ)將函數 的圖象向左平移
的圖象向左平移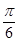 個單位,再向上平移1個單位,得到
個單位,再向上平移1個單位,得到 的圖象,即
的圖象,即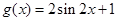 ,令
,令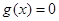 ,得:
,得: 或
或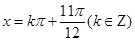 ,
,
易知每個周期上恰好有兩個零點,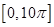 恰為
恰為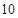 個周期,故
個周期,故 在
在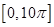 上有
上有 個零點.
個零點.
試題解析:(Ⅰ)由題意得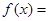


由周期為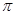 ,得
,得 . 得
. 得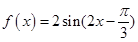
由正弦函數的單調增區間得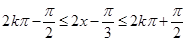 ,得
,得
所以函數 的單調增區間是
的單調增區間是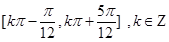 .
.
(Ⅱ)將函數 的圖象向左平移
的圖象向左平移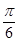 個單位,再向上平移1個單位,
個單位,再向上平移1個單位,
得到 的圖象,所以
的圖象,所以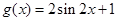
令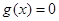 ,得:
,得: 或
或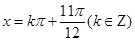
所以函數在每個周期上恰有兩個零點,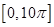 恰為
恰為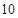 個周期,故
個周期,故 在
在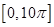 上有
上有 個零點.
個零點.
考點:1.三角函數的化簡與性質應用;2.三角函數的圖像變換;3.函數的零點.


科目:高中數學 來源: 題型:解答題
已知函數f(x)=sinx+cosx,f′(x)是f(x)的導函數,F(x)=f(x)f′(x)+f2(x)
(Ⅰ)求F(x)的最小正周期及單調區間;
(Ⅱ)求函數F(x)在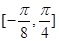 上的值域;
上的值域;
(Ⅲ)若f(x)=2f′(x),求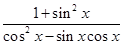 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com