
函數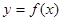 的定義域為
的定義域為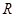 ,若存在常數
,若存在常數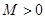 ,使得
,使得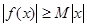 對一切實數
對一切實數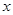 均成立,則稱
均成立,則稱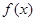 為“圓錐托底型”函數.
為“圓錐托底型”函數.
(1)判斷函數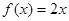 ,
,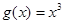 是否為“圓錐托底型”函數?并說明理由.
是否為“圓錐托底型”函數?并說明理由.
(2)若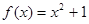 是“圓錐托底型” 函數,求出
是“圓錐托底型” 函數,求出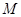 的最大值.
的最大值.
(3)問實數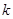 、
、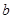 滿足什么條件,
滿足什么條件,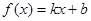 是“圓錐托底型” 函數.
是“圓錐托底型” 函數.
(1)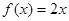 是,
是,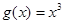 不是,(2)
不是,(2) ,(3)
,(3)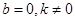
解析試題分析:(1)新定義問題,必須讀懂題意,嚴格按定義進行等價轉化.本題判斷函數是否為“圓錐托底型”函數,即判斷是否存在常數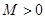 ,使得
,使得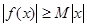 對一切實數
對一切實數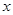 均成立,若成立必須證明,否則給出反例.本題解題關鍵在于常數
均成立,若成立必須證明,否則給出反例.本題解題關鍵在于常數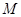 的確定.
的確定.  ,所以可確定常數
,所以可確定常數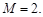 而由
而由 可知無論常數
可知無論常數 為什么正數,
為什么正數, 總能取較小的數比它小,即總能舉個反例,如當
總能取較小的數比它小,即總能舉個反例,如當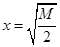 時,
時,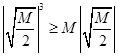 就不成立.(2)本題實質按新定義轉化為不等式恒成立問題:存在
就不成立.(2)本題實質按新定義轉化為不等式恒成立問題:存在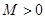 ,使得
,使得 對于任意實數恒成立.即當
對于任意實數恒成立.即當 時,
時, ,而
,而 取得最小值2,
取得最小值2,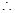
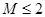 .(3)本題是討論滿足不等式恒成立的條件.即實數
.(3)本題是討論滿足不等式恒成立的條件.即實數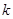 、
、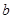 滿足什么條件,存在常數
滿足什么條件,存在常數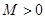 ,使得
,使得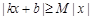 對一切實數
對一切實數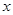 均成立.當
均成立.當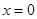 時,
時,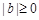 ,
,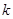 、
、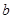 無限制條件;當
無限制條件;當 時,
時,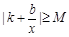 ,需
,需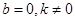 ,否則若
,否則若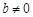 ,則當
,則當 時,
時,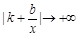 ,即
,即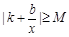 不能恒成立;若
不能恒成立;若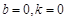 ,則
,則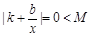 .
.
試題解析:(1). ,即對于一切實數
,即對于一切實數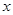 使得
使得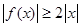 成立,
成立,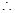
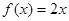 “圓錐托底型” 函數. 2分
“圓錐托底型” 函數. 2分
對于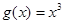 ,如果存在
,如果存在 滿足
滿足 ,而當
,而當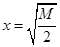 時,由
時,由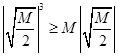 ,
,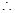
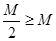 ,得
,得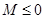 ,矛盾,
,矛盾,
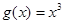 不是“圓錐托底型” 函數. 5分
不是“圓錐托底型” 函數. 5分
(2)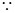
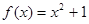 是“圓錐托底型” 函數,故存在
是“圓錐托底型” 函數,故存在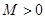 ,使得
,使得 對于任意實數恒成立.
對于任意實數恒成立.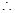 當
當 時,
時, ,此時當
,此時當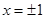 時,
時, 取得最小值2,
取得最小值2,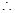
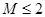 9分
9分
而當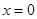 時,
時,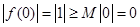 也成立.
也成立.
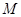 的最大值等于
的最大值等于 . 10分
. 10分
(


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:解答題
定義:對于函數 ,若存在非零常數
,若存在非零常數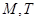 ,使函數
,使函數 對于定義域內的任意實數
對于定義域內的任意實數 ,都有
,都有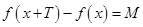 ,則稱函數
,則稱函數 是廣義周期函數,其中稱
是廣義周期函數,其中稱 為函數
為函數 的廣義周期,
的廣義周期, 稱為周距.
稱為周距.
(1)證明函數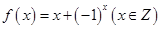 是以2為廣義周期的廣義周期函數,并求出它的相應周距
是以2為廣義周期的廣義周期函數,并求出它的相應周距 的值;
的值;
(2)試求一個函數 ,使
,使 (
( 為常數,
為常數,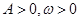 )為廣義周期函數,并求出它的一個廣義周期
)為廣義周期函數,并求出它的一個廣義周期 和周距
和周距 ;
;
(3)設函數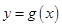 是周期
是周期 的周期函數,當函數
的周期函數,當函數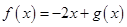 在
在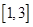 上的值域為
上的值域為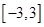 時,求
時,求 在
在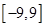 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數 的定義域為E,值域為F.
的定義域為E,值域為F.
(1)若E={1,2},判斷實數λ=lg22+lg2lg5+lg5﹣ 與集合F的關系;
與集合F的關系;
(2)若E={1,2,a},F={0, },求實數a的值.
},求實數a的值.
(3)若 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=(x+2)ln(x+1)-ax2-x(a∈R),g(x)=ln(x+1).
(1)若a=0,F(x)=f(x)-g(x),求函數F(x)的極值點及相應的極值.
(2)若對于任意x2>0,存在x1滿足x1<x2且g(x1)=f(x2)成立,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com