
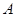 、
、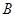 、
、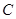 、
、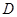 的坐標分別為
的坐標分別為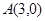 、
、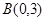 、
、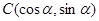 、
、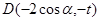 ,
,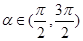
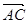 |=|
|=|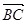 |,求角
|,求角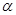 的值;
的值;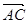 ·
·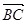 =
=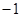 ,求
,求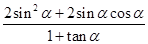 的值.
的值.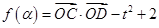 在定義域
在定義域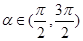 有最小值
有最小值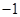 ,求
,求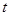 的值.
的值.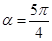 ;(2)
;(2)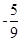 ;(3)
;(3)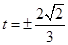 .
.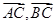 的坐標分別求得,即有
的坐標分別求得,即有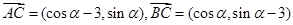 ,又根據
,又根據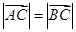 可以建立關于
可以建立關于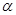 的方程,求得
的方程,求得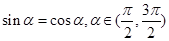 ,從而
,從而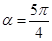 ;(2)由平面向量數量積的坐標表示,
;(2)由平面向量數量積的坐標表示,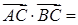
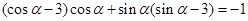 ,化簡可得
,化簡可得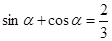 ,再將要求值的表達式化簡為
,再將要求值的表達式化簡為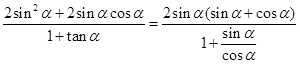
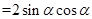 ,
,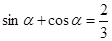 ,可求得
,可求得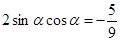 ,從而需求值的表達式的值為
,從而需求值的表達式的值為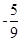 ;
;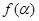
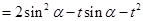 ,若令
,若令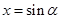 ,則問題等價于當
,則問題等價于當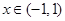 時,求使
時,求使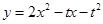 最小值為-1的
最小值為-1的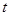 的值,顯然
的值,顯然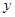 是關于
是關于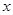 的開口向上的二次函數,若其在
的開口向上的二次函數,若其在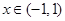 時,存在最小值,則必有對稱軸
時,存在最小值,則必有對稱軸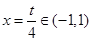 ,且當
,且當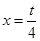 時,
時,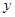 取到最小值-1,從而建立了關于
取到最小值-1,從而建立了關于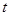 的方程,可解得
的方程,可解得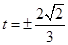 .
.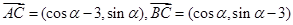 ,又∵
,又∵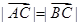 ,
,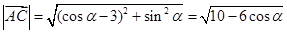 ,
,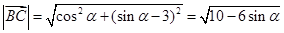
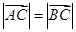 得
得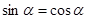 ,又
,又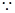
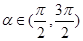 ,∴
,∴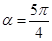 5分;
5分;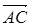 ·
·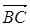 =
=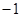 得
得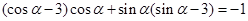 ,
,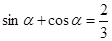 ① 6分
① 6分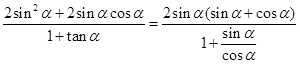
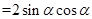 7分
7分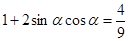 ∴
∴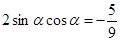 8分
8分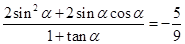 . 9分;
. 9分;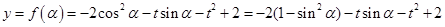
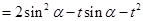 10分
10分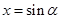 ,
, (
(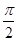 ,
,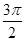 ),
),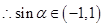 ,
,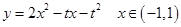 11分
11分 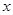 的二次函數開口向上,對稱軸為
的二次函數開口向上,對稱軸為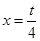 ,
,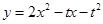 在
在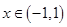 上存在最小值,則對稱軸
上存在最小值,則對稱軸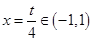
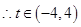 12分
12分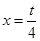 時,
時,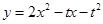 取最小值為
取最小值為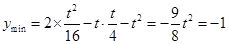
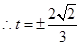 14分
14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com