
 萬元,每年應交保險費,養路費,保險費共
萬元,每年應交保險費,養路費,保險費共 萬元,汽車的維修費為:第一年
萬元,汽車的維修費為:第一年 萬元,第二年
萬元,第二年 萬元,第三年
萬元,第三年 萬元,……,依次成等差數列逐年遞增.
萬元,……,依次成等差數列逐年遞增. 年該車的總費用(包括購車費用)為
年該車的總費用(包括購車費用)為 試寫出
試寫出 的表達式;
的表達式; 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數學 來源:不詳 題型:解答題
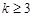 ,若項數為
,若項數為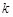 的數列
的數列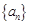 滿足:對任意的
滿足:對任意的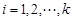 ,均有
,均有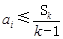 (其中
(其中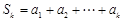 ),則稱數列
),則稱數列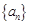 為“Γ數列”.
為“Γ數列”.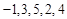 和
和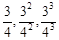 是否是“Γ數列”,并說明理由;
是否是“Γ數列”,并說明理由;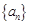 為“Γ數列”,求證:
為“Γ數列”,求證: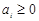 對
對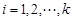 恒成立;
恒成立;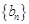 是公差為
是公差為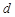 的無窮項等差數列,若對任意的正整數
的無窮項等差數列,若對任意的正整數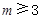 ,
,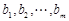
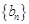 的公差
的公差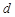 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com