
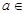 R,函數
R,函數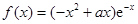 .(
.( R,e為自然對數的底數)
R,e為自然對數的底數)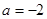 時,求函數
時,求函數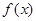 的單調遞減區間;
的單調遞減區間;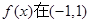 內單調遞減,求a的取值范圍;
內單調遞減,求a的取值范圍;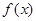 是否為R上的單調函數,若是,求出a的取值范圍;若不是,請說明理由.
是否為R上的單調函數,若是,求出a的取值范圍;若不是,請說明理由.
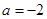 時,
時,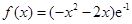
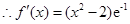 ……………………………………………………………………1分
……………………………………………………………………1分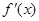
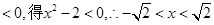 ……………………………………………2分
……………………………………………2分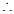
 (-
(-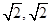 ).
).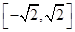 也對) ………………………………………………………3分
也對) ………………………………………………………3分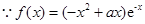
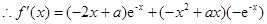
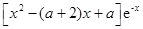 . ………………………………………………………………4分
. ………………………………………………………………4分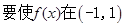 上單調遞減,
上單調遞減,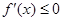 對
對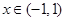 都成立,
都成立,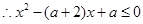 對
對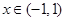 都成立.…………………………………………5分
都成立.…………………………………………5分 ,則
,則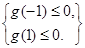 …………………………………………………………………………7分
…………………………………………………………………………7分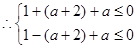
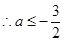 .
. (注:不帶等號扣1分) ………………………………………………8分
(注:不帶等號扣1分) ………………………………………………8分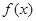 在R上單調遞減,則
在R上單調遞減,則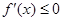 對
對 R 都成立
R 都成立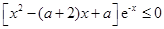 對
對 R都成立.…………………………………………9分
R都成立.…………………………………………9分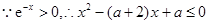 對
對 R都成立
R都成立 ,
,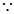 圖象開口向上
圖象開口向上 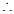 不可能對
不可能對 R都成立
R都成立 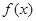 在R上單調遞減,則
在R上單調遞減,則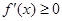 對
對 R都成立,
R都成立,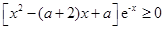 對
對 R都成立,
R都成立,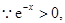
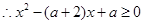 對
對 R都成立.
R都成立.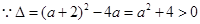
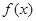 不可能在R上單調遞增.
不可能在R上單調遞增.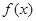 不可能是R上的單調函數
不可能是R上的單調函數

 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源:不詳 題型:解答題
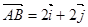 (
(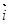 、
、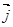 分別是與x、y軸正半軸同方向的單位向量), 函數g(x)=x2-x-6.
分別是與x、y軸正半軸同方向的單位向量), 函數g(x)=x2-x-6. 的最小值.
的最小值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
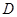 上的函數
上的函數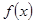 對
對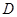 上的任意
上的任意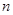 個值
個值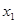 ,
,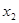 ,…,
,…,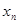 ,總滿足
,總滿足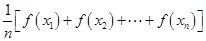 ≤
≤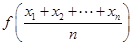 ,則稱
,則稱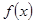 為
為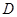 上的凸函數.已知函數
上的凸函數.已知函數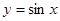 在區間
在區間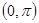 上是“凸函數”,則在
上是“凸函數”,則在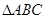 中,
中,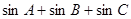 的最大值是___________
的最大值是___________查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
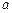 、
、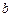 萬元,則農民購買家電產品獲得的補貼分別為
萬元,則農民購買家電產品獲得的補貼分別為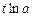 萬元、
萬元、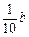 萬元(
萬元(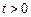 且為常數).已知該企業投放總價值為100萬元的A、B兩種型號的家電產品,且A、B兩種型號的投放金額都不低于10萬元.
且為常數).已知該企業投放總價值為100萬元的A、B兩種型號的家電產品,且A、B兩種型號的投放金額都不低于10萬元.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com