
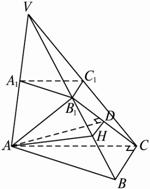
(1)求證直線B
(2)求點(diǎn)A到平面VBC的距離;
(3)求二面角A—VB—C的大小.
解法一:(1)證明:∵平面A1B
∴B
∴B
又∵平面AB
平面AB
∴BC⊥平面AB
∴BC⊥AB1,?
∴B

又A
B
∴B
(2)解法1:過A作AD⊥B
∵△AB
∴D為B
∵BC⊥平面AB
∴BC⊥AD.又B
∴AD⊥平面VBC,?
∴線段AD的長即為點(diǎn)A到平面VBC的距離.?
在正△AB![]() ·AC=
·AC=![]() ×2a=
×2a=![]() a.?
a.?
∴點(diǎn)A到平面VBC的距離為![]() .?
.?
解法2:取AC中點(diǎn)O連結(jié)B1O,則B1O⊥平面ABC,且B1O=![]() a.?
a.?
由(1)知BC⊥B
∴![]() ,?
,?
即![]() ×
×![]() BC
BC![]() AC
AC![]() B1O=
B1O=![]() ×
×![]() BC
BC![]() B1C
B1C![]() x.?
x.?
解得x=![]() a,?
a,?
即A到平面VBC的距離為![]() a.?
a.?
(3)解:過D點(diǎn)作DH⊥VB于H,連AH,由三垂線定理知AH⊥VB,?
∴∠AHD是二面角A—VB—C的平面角.?
在Rt△AHD中,?
AD=![]() a,△B1DH∽△B1BC,
a,△B1DH∽△B1BC,![]() =
=![]() .?
.?
∴DH=![]() =
=![]() a.?
a.?
∴tan∠AHD=![]() =
=![]() .?
.?
∴∠AHD=arctan![]() .?
.?
所以,二面角A—VB—C的大小為arctan![]() .
.
解法二:取AC中點(diǎn)O連B1O,已知OB1⊥底面ABC,過O從直線OE∥BC交AB于E.?
取O為空間直角坐標(biāo)系的原點(diǎn),OE,OC,OB1所在直線分別為x軸,y軸,z軸建立如圖所示的空間直角坐標(biāo)系.?

則A(0,-a,0),B(a,a,0),C(0,a,0),B1(0,0,![]() a).??
a).??
(1) 證明:∵![]() =(-a,0,0),
=(-a,0,0),![]() =(0,a,
=(0,a,![]() a),?
a),?
∴![]()
![]()
![]() =(-a,0,0)·(0,a,
=(-a,0,0)·(0,a, ![]() a)=0,?
a)=0,?
∴![]() ⊥
⊥![]() ,?
,?
∴BC⊥AB1.?
又∵B
B
由已知BC⊥AC,?
AC∥A
而BC∥B
∴B
(2)解:設(shè)平面VBC的一個(gè)法向量n=(x,y,z).?
又![]() =(0,-a,
=(0,-a,![]() a)?
a)?
由
取z=1 得n=(0,![]() ,1).?
,1).?
點(diǎn)A到平面VBC的距離,即![]() 在平面VBC的法向量n上的投影的絕對(duì)值.
在平面VBC的法向量n上的投影的絕對(duì)值.
∵![]() =(0,a,
=(0,a,![]() a),設(shè)所求距離為d.?
a),設(shè)所求距離為d.?
則d=||![]() |·cos〈
|·cos〈![]() ·n〉|?
·n〉|?
||![]() |·
|· |
|
=![]() =
=![]() a.?
a.?
所以,A到平面VBC的距離為![]() a.?
a.?
(3)解:設(shè)平面VAB的一個(gè)法向量m=(x1,y1,z1),?
由
取z1=1,m=(2![]() ,-
,-![]() ,1).?
,1).?
∴cos〈m,n〉=![]() =-
=-![]() .?
.?
∵二面角A—VB—C為銳角,
∴二面角A—VB—C的大小為arccos![]() .
.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
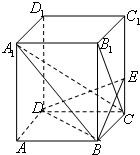 如圖,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,
如圖,已知正四棱柱ABCD-A1B1C1D1中,2AB=BB1,查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
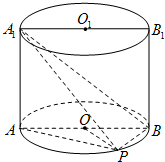 如圖,已知點(diǎn)P在圓柱OO1的底面圓O上,AB為圓O的直徑,圓柱OO1的表面積為20π,OA=2,∠AOP=120°.
如圖,已知點(diǎn)P在圓柱OO1的底面圓O上,AB為圓O的直徑,圓柱OO1的表面積為20π,OA=2,∠AOP=120°.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
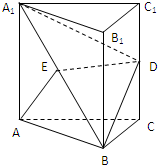 如圖,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分別為CC1、A1B的中點(diǎn).
如圖,已知正三棱柱ABC-A1B1C1,AA1=AB=2a,D、E分別為CC1、A1B的中點(diǎn).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知正四棱柱ABCD-A1B1C1D1中,底面邊長AB=2,側(cè)棱BB1的長為4,過點(diǎn)B作B1C的垂線交側(cè)棱CC1于點(diǎn)E,交B1C于點(diǎn)F.
如圖,已知正四棱柱ABCD-A1B1C1D1中,底面邊長AB=2,側(cè)棱BB1的長為4,過點(diǎn)B作B1C的垂線交側(cè)棱CC1于點(diǎn)E,交B1C于點(diǎn)F.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,已知棱長為1的正方體ABCD-A1B1C1D1.
如圖,已知棱長為1的正方體ABCD-A1B1C1D1.| B1Q | QD |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com