
| A、e12+e22=2 | ||||||||
| B、e12+e22=4 | ||||||||
C、
| ||||||||
D、
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|


 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
| A.e12+e22=2 | B.e12+e22=4 | ||||||||||||||||
C.
| D.
|
查看答案和解析>>
科目:高中數學 來源: 題型:
已知F1、F2是兩個定點,點P是以F1和F2為公共焦點的橢圓和雙曲線的一個交點,并且PF1⊥PF2,e1和e2分別是上述橢圓和雙曲線的離心率,則有
A.![]() +
+![]() =4
=4 ![]() B.
B.![]() +
+![]() =2
=2
C.e12+e22=4 D.e12+e22=2
查看答案和解析>>
科目:高中數學 來源:2003-2004學年江蘇省無錫市天一中學高二(下)期末數學試卷(強化班)(解析版) 題型:選擇題
 ,那么橢圓C1的離心率為( )
,那么橢圓C1的離心率為( )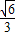



查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com