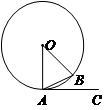(本小題滿分10分)選修4-1:幾何證明與選講
如圖,

為直角三角形,
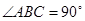
,以

為直徑的圓交
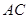
于點

,點

是

邊的中點,連

交圓

于點

.

(1)求證:

四點共圓;
(2)求證:
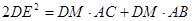
.
(1)證明四邊形OBDE的對角互補即可.本小題只需要證明:

.
(2) 延長

交圓于點

.可知


,
再根據(jù)DO為三角形ABC的中位線,OH等于AB的一半即可證明.
證明:(1)連接

,則

----------------1分
又

是

的中點,所以

----------------3分
又

,所以

,所以

故

四點共圓. -------------5分
(2) 延長

交圓于點

.


------------8分

,即

--------10分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
已知圓的方程為
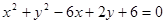
,則其圓心坐標和半徑分別為( )
| A.(3, -1),r = 4 | B.(3, -1),r = 2 |
| C.(-3, 1),r = 2 | D.(-3, 1),r = 4 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知x
2+y
2=10, 則3x+4y的最大值為( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知圓

的圓心在直線

上,且圓

與

軸相切,若圓

截直線

得弦長為

,求圓

的方程.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如右圖,A、B是⊙O上的兩點,AC是⊙O的切線,∠B=70°,則∠BAC等于
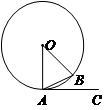
A. 70° B. 35° C. 20° D. 10°
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
圓心為點

,且過點

的圓的方程為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知圓系

(a≠1,a∈R),則該圓系恒過定點
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,圓內(nèi)的兩條弦

,

相交于圓內(nèi)一點

,已知

,

,
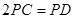
,則

的長為

查看答案和解析>>

 為直角三角形,
為直角三角形,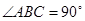 ,以
,以 為直徑的圓交
為直徑的圓交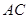 于點
于點 ,點
,點 是
是 邊的中點,連
邊的中點,連 交圓
交圓 于點
于點 .
.
 四點共圓;
四點共圓;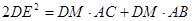 .
.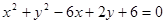 ,則其圓心坐標和半徑分別為( )
,則其圓心坐標和半徑分別為( )