
已知橢圓 的左、右焦點分別為
的左、右焦點分別為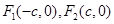 ,若橢圓上存在一點
,若橢圓上存在一點 使
使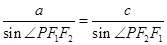 ,則該橢圓的離心率的取值范圍為 .
,則該橢圓的離心率的取值范圍為 .
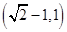
解析試題分析:在△PF1F2中,由正弦定理得: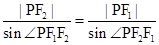 ,則由已知得:
,則由已知得: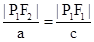 ,
,
即:a|PF1|=|cPF2|
設點(x0,y0)由焦點半徑公式,
得:|PF1|=a+ex0,|PF2|=a-ex0,則a(a+ex0)=c(a-ex0)
解得:x0=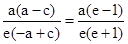 ,由橢圓的幾何性質知:x0>-a則
,由橢圓的幾何性質知:x0>-a則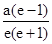 >-a
>-a
整理得e2+2e-1>0,解得:e<-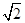 -1或e>
-1或e>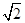 -1,又e∈(0,1),
-1,又e∈(0,1),
故橢圓的離心率:e∈(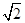 -1,1),故答案為:(
-1,1),故答案為:(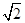 -1,1).
-1,1).
考點:本題主要考查了橢圓的定義,性質及焦點三角形的應用,特別是離心率應是橢圓考查的一個亮點,多數是用a,b,c轉化,用橢圓的范圍來求解離心率的范圍.
點評:解決該試題的關鍵是能通過橢圓的定義以及焦點三角形的性質得到a,b,c的關系式的轉換,進而得到離心率的范圍。


科目:高中數學 來源: 題型:填空題
①若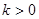 ,則方程
,則方程 有實根;
有實根;
②“若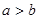 ,則
,則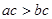 ”的否命題;
”的否命題;
③“矩形的對角線相等”的逆命題;
④“若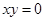 ,則
,則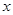 、
、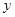 至少有一個為零”的逆否命題 .
至少有一個為零”的逆否命題 .
以上命題中的真命題有_______________。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com