
(12分) 已知函數 =loga
=loga (a>0且a≠1)是奇函數
(a>0且a≠1)是奇函數
(1)求 ,(
,(
(2)討論 在(1,+∞)上的單調性,并予以證明
在(1,+∞)上的單調性,并予以證明
(1)
(2)當a>1時,f(x)=loga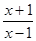 在(1,+∞)上為減函數;當0<a<1時,f(x)=loga
在(1,+∞)上為減函數;當0<a<1時,f(x)=loga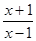 在(1,+∞)上為增函數
在(1,+∞)上為增函數
【解析】解:
(1)
(2)設u=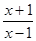 ,任取x2>x1>1,則
,任取x2>x1>1,則
u2-u1=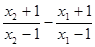
=
=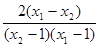 .
.
∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴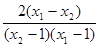 <0,即u2<u1.
<0,即u2<u1.
當a>1時,y=logax是增函數,∴logau2<logau1,
即f(x2)<f(x1);
當0<a<1時,y=logax是減函數,∴logau2>logau1,
即f(x2)>f(x1).
綜上可知,當a>1時,f(x)=loga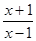 在(1,+∞)上為減函數;當0<a<1時,f(x)=loga
在(1,+∞)上為減函數;當0<a<1時,f(x)=loga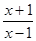 在(1,+∞)上為增函數.
在(1,+∞)上為增函數.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
| π | 2 |
查看答案和解析>>
科目:高中數學 來源:2011年江西省高一上學期期中考試數學 題型:解答題
(本小題滿分12分)
已知函數 的定義域為集合A,
的定義域為集合A,  的值域為集合B.
的值域為集合B.
(1)若 ,求
,求 ;
;
(2) 若 ,求實數
,求實數 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年新疆烏魯木齊一中高三上學期第三次月考數學文試題 題型:解答題
(本小題滿分12分)
已知函數 的導函數
的導函數 ,數列
,數列 的前
的前 項和為
項和為 ,點
,點 均在函數
均在函數 的圖象上.
的圖象上.
(Ⅰ)求數列 的通項公式及
的通項公式及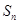 的最大值;
的最大值;
(Ⅱ)令 ,其中
,其中 ,求
,求 的前
的前 項和.
項和.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年山東省高三上學期第一次診斷性測試文科數學卷 題型:解答題
(本小題滿分12分)已知函數 是偶函數.
是偶函數.
(1)求k的值;
(2)若方程 有解,求m的取值范圍.
有解,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com