
在(a-2b)![]() 的展開式中,
的展開式中,
(1) 若n=10,求展開式的倒數第四項(要求將系數計算到具體數值)
(2) 若展開式中二項式系數不超過6的項恰好有5項,求n的值;
(3) 若展開式中系數不超過6的項恰好有五項,求n的值。
解析:(1)(a-2b)![]() 展開式的通項公式(即第r+1項)是:
展開式的通項公式(即第r+1項)是:![]()
n=10時,展開式共有11項,其倒數第四項即第八項。
![]()
(2)展開式中二項式系數不超過6的項恰好有5項,
一方面說明![]() ,5項存在。
,5項存在。
另一方面說明展開式的第二項的二項式系數也不超過6,即![]()
當n=4時,各項的二項式系數分別是1,4,6,4,1,恰好有5項二項式系數不超過6。
當n=5,各項的二項式系數分別是1,5,10,10,5,1,沒有5項二項式系數不超過6.
當n=6,各項的二項式系數分別是1,6,15,20,15,6,1,沒有5項的二項式系數不超過6.
所以,所求n的值等于4.
(3) 展開式第r+1項的系數是![]()
展開式種的第一項系數等于1,不超過6;
要展開式有5項,![]()
展開式種所有偶數項的習俗均為負,故偶數項不能超過4項,即![]()
當n=4時,各項的習俗分別是1,-8,24,-32,16,沒有5項系數不超過6.
類似地,n=5,n=6時,展開式種都沒有5項系數不超過6.
當n=7時,第1,2,4,6,8項的習俗不超過6.
當n=8時,第1,2,4,6,8項的習俗不超過6.
所以,所求n的值等于7或者8.、


 新思維寒假作業(yè)系列答案
新思維寒假作業(yè)系列答案科目:高中數學 來源: 題型:
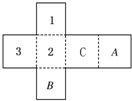 如圖是一個正方體盒子的平面展開圖,在其中的兩個正方形內標有數字1、2、3,要在其余正方形內分別填上-1、-2、-3,使得按虛線折成正方體后,相對面上的兩數互為相反數,則A處應填( )
如圖是一個正方體盒子的平面展開圖,在其中的兩個正方形內標有數字1、2、3,要在其余正方形內分別填上-1、-2、-3,使得按虛線折成正方體后,相對面上的兩數互為相反數,則A處應填( )查看答案和解析>>
科目:高中數學 來源: 題型:單選題
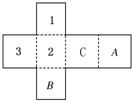 如圖是一個正方體盒子的平面展開圖,在其中的兩個正方形內標有數字1、2、3,要在其余正方形內分別填上-1、-2、-3,使得按虛線折成正方體后,相對面上的兩數互為相反數,則A處應填
如圖是一個正方體盒子的平面展開圖,在其中的兩個正方形內標有數字1、2、3,要在其余正方形內分別填上-1、-2、-3,使得按虛線折成正方體后,相對面上的兩數互為相反數,則A處應填查看答案和解析>>
科目:高中數學 來源:2012-2013學年貴州省安順學院附中高二(上)期中數學試卷(理科)(解析版) 題型:選擇題
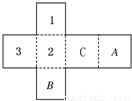
查看答案和解析>>
科目:高中數學 來源:2012-2013學年貴州省安順學院附中高二(上)期中數學試卷(理科)(解析版) 題型:選擇題
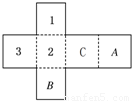
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com