
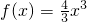 +ax-1(a∈R),其中f'(x)是f(x)的導函數.
+ax-1(a∈R),其中f'(x)是f(x)的導函數.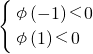 即
即 解得
解得 .
. 時,對一切|a|≤1,都有g(x)<0恒成立.
時,對一切|a|≤1,都有g(x)<0恒成立.

 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
| a |
| x+1 |
| 9 |
| 2 |
| g(x2)-g(x1) |
| x2-x1 |
| 1 |
| ?(x) |
查看答案和解析>>
科目:高中數學 來源:2009-2010學年黑龍江省哈爾濱三中高二(下)第二次段考數學試卷(文科)(解析版) 題型:解答題
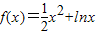
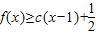 ,求c的取值范圍.
,求c的取值范圍.查看答案和解析>>
科目:高中數學 來源:2011年湖北省荊州市松滋二中高考數學限時訓練(解析版) 題型:解答題
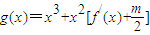 在區間(t,3)上有最值,求實數m取值范圍;
在區間(t,3)上有最值,求實數m取值范圍;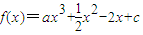
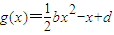 ,在(1)的條件下,是否存在實數b,使得函數g(x)的圖象與函數f(x)的圖象恒有含x=-1的三個不同交點?若存在,求出實數b的取值范圍;否則說明理由.
,在(1)的條件下,是否存在實數b,使得函數g(x)的圖象與函數f(x)的圖象恒有含x=-1的三個不同交點?若存在,求出實數b的取值范圍;否則說明理由.查看答案和解析>>
科目:高中數學 來源:2008年北京市朝陽區高考數學二模試卷(文科)(解析版) 題型:解答題
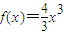 +ax-1(a∈R),其中f'(x)是f(x)的導函數.
+ax-1(a∈R),其中f'(x)是f(x)的導函數.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com