
(2007
江西,21)設(shè)動點P到點A(-1,0)和B(1,0)的距離分別為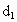 和
和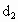 ,∠APB=2θ,且存在常數(shù)λ(0<λ<1),使得
,∠APB=2θ,且存在常數(shù)λ(0<λ<1),使得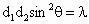 .
.
(1)
證明:動點P的軌跡C為雙曲線,并求出C的方程;(2)
過點B作直線交雙曲線C的右支于M、N兩點,試確定λ的范圍,使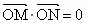 ,其中點O為坐標(biāo)原點.
,其中點O為坐標(biāo)原點. |
解析:解法一: (1)在△PAB中,|AB|=2,則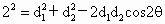 , ,
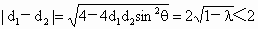 (常數(shù)), (常數(shù)),
點 P的軌跡C是以A、B為焦點,實軸長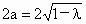 的雙曲線,方程為 的雙曲線,方程為 . .
(2) 設(shè)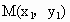 , , . .
①當(dāng) MN垂直于x軸時,MN的方程為x=1,M(1,1),N(1,-1)在雙曲線上,即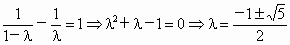 , ,
因為 0<λ<1,所以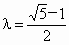 . .
②當(dāng) MN不垂直于x軸時,設(shè)MN的方程為y=k(x-1).由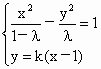 得: 得: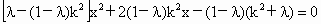 , ,
由題意知:  , ,
所以 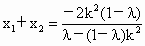 , ,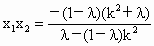 , ,
于是: 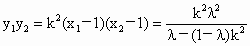 , ,
因為 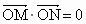 ,且M,N在雙曲線右支上, ,且M,N在雙曲線右支上,
所以
由①②知, 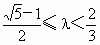 . .
解法二: (1)同解法一(2) 設(shè)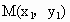 , , ,MN的中點為 ,MN的中點為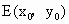 . .
①當(dāng) 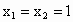 時, 時,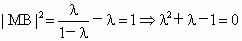 , ,
因為 0<λ<1,所以 ; ;
②當(dāng) 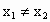 時, 時,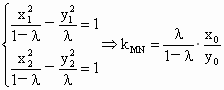 . .
又 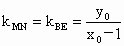 .所以 .所以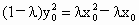 ; ;
由 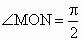 得 得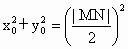 ,由第二定義得 ,由第二定義得
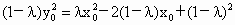 . .
于是由 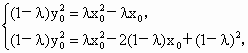 得 得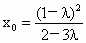 . .
因為 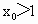 ,所以 ,所以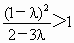 , ,
又 0<λ<1,解得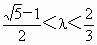 . .
由①②知 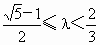 . . |
|
剖析:本題考查雙曲線的性質(zhì)以及參數(shù)方程的解法. |


國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com