
正方形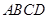 的邊長(zhǎng)為2,
的邊長(zhǎng)為2,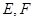 分別為邊
分別為邊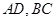 的中點(diǎn),
的中點(diǎn),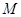 是線段
是線段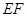 的中點(diǎn),如圖,把正方形沿
的中點(diǎn),如圖,把正方形沿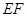 折起,設(shè)
折起,設(shè)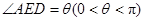 .
.
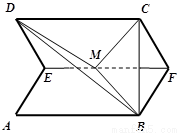
(1)求證:無(wú)論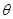 取何值,
取何值,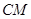 與
與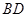 不可能垂直;
不可能垂直;
(2)設(shè)二面角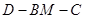 的大小為
的大小為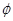 ,當(dāng)
,當(dāng)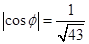 時(shí),求
時(shí),求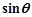 的值.
的值.
(1)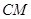 與
與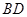 不可能垂直; (2)
不可能垂直; (2)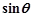 的值為
的值為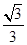 .
.
【解析】
試題分析:(1)假設(shè)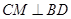 , 1分
, 1分
又因?yàn)?img
src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2013081212481339154979/SYS201308121248470798445435_DA.files/image006.png">,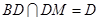 ,所以
,所以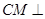 平面
平面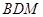 ,
3分
,
3分
所以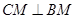 ,又
,又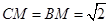 ,所以
,所以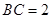 , 5分
, 5分
這與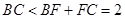 矛盾,所以假設(shè)不成立,所以
矛盾,所以假設(shè)不成立,所以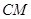 與
與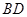 不可能垂直; 6分
不可能垂直; 6分
(2)分別以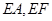 為
為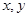 軸,過(guò)點(diǎn)
軸,過(guò)點(diǎn)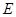 垂直平面
垂直平面 向上為
向上為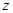 軸,如圖建立坐標(biāo)系,
軸,如圖建立坐標(biāo)系,
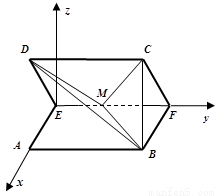
設(shè)平面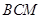 的一個(gè)法向量為
的一個(gè)法向量為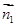 ,
,
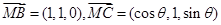 ,
,
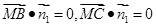 , 7分
, 7分
得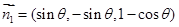 , 8分
, 8分
設(shè)平面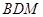 的一個(gè)法向量為
的一個(gè)法向量為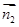 ,
,
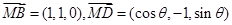 ,
,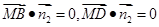 , 9分
, 9分
得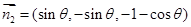 , 10分
, 10分
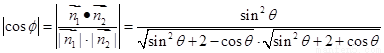 11分
11分
=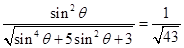 , 12分
, 12分
得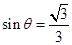 , 13分
, 13分
所以當(dāng)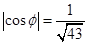 時(shí),
時(shí),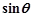 的值為
的值為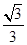 . 14分
. 14分
考點(diǎn):折疊問(wèn)題,平行關(guān)系,垂直關(guān)系,角的計(jì)算。
點(diǎn)評(píng):中檔題,立體幾何問(wèn)題中,平行關(guān)系、垂直關(guān)系,角、距離、面積、體積等的計(jì)算,是常見(jiàn)題型,基本思路是將空間問(wèn)題轉(zhuǎn)化成為平面問(wèn)題,利用平面幾何知識(shí)加以解決。要注意遵循“一作,二證,三計(jì)算”。利用“向量法”,通過(guò)建立空間直角坐標(biāo)系,往往能簡(jiǎn)化解題過(guò)程。對(duì)于折疊問(wèn)題,首先要弄清“變”與“不變”的幾何元素。


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
 如圖所示,過(guò)正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的邊長(zhǎng)為2,OP=2,連接AP、BP、CP、DP,M、N分別是AB、BC的中點(diǎn),以O(shè)為原點(diǎn),射線OM、ON、OP分別為Ox軸、Oy軸、Oz軸的正方向建立空間直角坐標(biāo)系.若E、F分別為PA、PB的中點(diǎn),求A、B、C、D、E、F的坐標(biāo).
如圖所示,過(guò)正方形ABCD的中心O作OP⊥平面ABCD,已知正方形的邊長(zhǎng)為2,OP=2,連接AP、BP、CP、DP,M、N分別是AB、BC的中點(diǎn),以O(shè)為原點(diǎn),射線OM、ON、OP分別為Ox軸、Oy軸、Oz軸的正方向建立空間直角坐標(biāo)系.若E、F分別為PA、PB的中點(diǎn),求A、B、C、D、E、F的坐標(biāo).查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年廣東省廣州市畢業(yè)班綜合測(cè)試(二)理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知正方形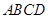 的邊長(zhǎng)為2,
的邊長(zhǎng)為2,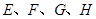 分別是邊
分別是邊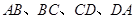 的中點(diǎn).
的中點(diǎn).
(1)在正方形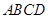 內(nèi)部隨機(jī)取一點(diǎn)
內(nèi)部隨機(jī)取一點(diǎn)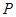 ,求滿(mǎn)足
,求滿(mǎn)足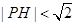 的概率;
的概率;
(2)從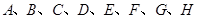 這八個(gè)點(diǎn)中,隨機(jī)選取兩個(gè)點(diǎn),記這兩個(gè)點(diǎn)之間的距離為
這八個(gè)點(diǎn)中,隨機(jī)選取兩個(gè)點(diǎn),記這兩個(gè)點(diǎn)之間的距離為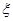 ,求隨機(jī)變量
,求隨機(jī)變量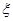 的分布列與數(shù)學(xué)期望
的分布列與數(shù)學(xué)期望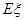 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2012-2013學(xué)年江西省高三最后一次模擬考試文科數(shù)學(xué)試卷(解析版) 題型:解答題
已知正方形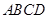 的邊長(zhǎng)為2,
的邊長(zhǎng)為2,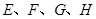 分別是邊
分別是邊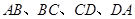 的中點(diǎn).
的中點(diǎn).
(1)在正方形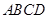 內(nèi)部隨機(jī)取一點(diǎn)
內(nèi)部隨機(jī)取一點(diǎn)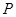 ,求滿(mǎn)足
,求滿(mǎn)足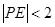 的概率;
的概率;
(2)從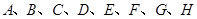 這八個(gè)點(diǎn)中,隨機(jī)選取兩個(gè)點(diǎn),記這兩個(gè)點(diǎn)之間的距離的平方為
這八個(gè)點(diǎn)中,隨機(jī)選取兩個(gè)點(diǎn),記這兩個(gè)點(diǎn)之間的距離的平方為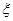 ,求
,求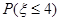 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年深圳市高三第一次調(diào)研考試數(shù)學(xué)文卷 題型:解答題
(本題滿(mǎn)分12分)
如圖,有一正方形鋼板 缺損一角(圖中的陰影部分),邊緣線
缺損一角(圖中的陰影部分),邊緣線 是以直線AD為對(duì)稱(chēng)軸,以線段
是以直線AD為對(duì)稱(chēng)軸,以線段 的中點(diǎn)
的中點(diǎn) 為頂點(diǎn)的拋物線的一部分.工人師傅要將缺損一角切割下來(lái),使剩余的部分成為一個(gè)直角梯形.若正方形的邊長(zhǎng)為2米,問(wèn)如何畫(huà)切割線
為頂點(diǎn)的拋物線的一部分.工人師傅要將缺損一角切割下來(lái),使剩余的部分成為一個(gè)直角梯形.若正方形的邊長(zhǎng)為2米,問(wèn)如何畫(huà)切割線 ,可使剩余的直角梯形的面積最大?并求其最大值.
,可使剩余的直角梯形的面積最大?并求其最大值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2007年普通高等學(xué)校招生全國(guó)統(tǒng)一考試?yán)砜茢?shù)學(xué)卷(海南) 題型:解答題
(本小題滿(mǎn)分12分)
如圖,面積為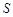 的正方形
的正方形 中有一個(gè)不規(guī)則的圖形M,可按下面方法估計(jì)M的面積:在正方形
中有一個(gè)不規(guī)則的圖形M,可按下面方法估計(jì)M的面積:在正方形 中隨機(jī)投擲
中隨機(jī)投擲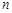 個(gè)點(diǎn),若
個(gè)點(diǎn),若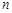 個(gè)點(diǎn)中有
個(gè)點(diǎn)中有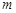 個(gè)點(diǎn)落入M中,則M的面積的估計(jì)值為
個(gè)點(diǎn)落入M中,則M的面積的估計(jì)值為 . 假設(shè)正方形
. 假設(shè)正方形 的邊長(zhǎng)為2,M的面積為1,并向正方形
的邊長(zhǎng)為2,M的面積為1,并向正方形 中隨機(jī)投擲10 000個(gè)點(diǎn),以
中隨機(jī)投擲10 000個(gè)點(diǎn),以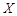 表示落入M中的點(diǎn)的數(shù)目.
表示落入M中的點(diǎn)的數(shù)目.
(Ⅰ)求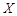 的均值
的均值 ;
;
 (Ⅱ)求用以上方法估計(jì)M的面積時(shí),M的面積的估計(jì)值與實(shí)際值之差在區(qū)間
(Ⅱ)求用以上方法估計(jì)M的面積時(shí),M的面積的估計(jì)值與實(shí)際值之差在區(qū)間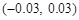 內(nèi)的概率.
內(nèi)的概率.
附表:
|
|
2424 |
2425 |
2574 |
2575 |
|
|
0.0403 |
0.0423 |
0.9570 |
0.9590 |
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com