
(1)試證:若m、n∈N*且m<n,則f(n)≥f(m)+![]() ,并指出取等號的條件;
,并指出取等號的條件;
(2)計(jì)算得f(2)=![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)>![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)>![]() ,觀察上述結(jié)果,推測一般的不等式,并用數(shù)學(xué)歸納法證明.
,觀察上述結(jié)果,推測一般的不等式,并用數(shù)學(xué)歸納法證明.
(1)證明:由m<n,得
f(n)-f(m)=(1+![]() +…+
+…+![]() )-(1+
)-(1+![]() +…+
+…+![]() )=
)=![]() +
+![]() +…+
+…+![]() ≥
≥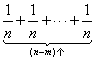 =
=![]() .
.
∴f(n)≥f(m)+![]() ,其中當(dāng)且僅當(dāng)n-m=1時(shí),等號成立.
,其中當(dāng)且僅當(dāng)n-m=1時(shí),等號成立.
(2)解:由f(2)≥![]() ,f(22)>2=
,f(22)>2=![]() ,f(8)=f(23)>
,f(8)=f(23)>![]() ,f(16)=f(24)>3=
,f(16)=f(24)>3=![]() ,f(32)=f(25)>
,f(32)=f(25)>![]() ,推測當(dāng)n∈N*時(shí),f(2n)≥
,推測當(dāng)n∈N*時(shí),f(2n)≥![]() ,下面用數(shù)學(xué)歸納法證明:
,下面用數(shù)學(xué)歸納法證明:
①當(dāng)n=2時(shí),f(22)=![]() >
>![]() ,不等式成立.
,不等式成立.
②假設(shè)n=k(k≥2)時(shí),不等式成立,即f(2k)≥![]() .
.
那么f(2k+1)≥f(2k)+![]() ≥
≥![]() +
+![]() =
=![]() =
=![]() ,
,
即當(dāng)n=k+1時(shí),f(2k+1)≥![]() ,命題成立.
,命題成立.
根據(jù)①②可得對于n≥2的自然數(shù)n命題成立.


 超能學(xué)典應(yīng)用題題卡系列答案
超能學(xué)典應(yīng)用題題卡系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| a2x+1 |
| 3x-1 |
| Sn |
| Tn |
| an |
| bn |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| an |
| 2 |
| f(n)-1 |
| f(n)+1 |
| n3 |
| n3+1 |
| n |
 |
| k=1 |
| 1 |
| f(k)-f(2k) |
| 27 |
| 4 |
| f(1)-f(n) |
| f(0)-f(1) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:成功之路·突破重點(diǎn)線·數(shù)學(xué)(學(xué)生用書) 題型:047
設(shè)n為自然數(shù),f(n)=1+![]() +
+![]() +…+
+…+![]()
(1)試證:若m、n∈N*且m<n,則f(n)≥f(m)+![]() ,并指出取等號的條件;
,并指出取等號的條件;
(2)計(jì)算得f(2)=![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)>![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)>![]() ,觀察上述結(jié)果,推測一般的不等式,并用數(shù)學(xué)歸納法證明.
,觀察上述結(jié)果,推測一般的不等式,并用數(shù)學(xué)歸納法證明.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com