
已知定點A(-1,0),F(xiàn)(2,0),定直線l:x= ,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
(Ⅰ)求E的方程;
(Ⅱ)試判斷以線段MN為直徑的圓是否過點F,并說明理由
解:(1)設P(x,y),則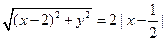
化簡得x2- =1(y≠0)…………………………………………4分
=1(y≠0)…………………………………………4分
(2)①當直線BC與x軸不垂直時,設BC的方程為y=k(x-2)(k≠0)
與雙曲線x2- =1聯(lián)立消去y得
=1聯(lián)立消去y得
(3-k)2x2+4k2x-(4k2+3)=0
由題意知3-k2≠0且△>0
設B(x1,y1),C(x2,y2),
則
y1y2=k2(x1-2)(x2-2)=k2[x1x2-2(x1+x2)+4]
=k2( +4)
+4)
=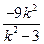
因為x1、x2≠-1
所以直線AB的方程為y=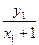 (x+1)
(x+1)
因此M點的坐標為( )
)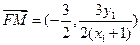 ,同理可得
,同理可得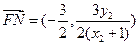
因此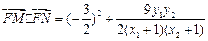
=
=0
②當直線BC與x軸垂直時,起方程為x=2,則B(2,3),C(2,-3)
AB的方程為y=x+1,因此M點的坐標為(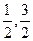 ),
),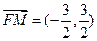
同理可得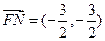
因此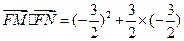 =0
=0
綜上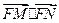 =0,即FM⊥FN
=0,即FM⊥FN
故以線段MN為直徑的圓經(jīng)過點F
解析


科目:高中數(shù)學 來源: 題型:
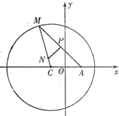 如圖,已知定點A(1,0),定圓C:(x+1)2+y2=8,M為圓C上的一個動點,點P在線段AM上,點N在線段CM上,且滿足
如圖,已知定點A(1,0),定圓C:(x+1)2+y2=8,M為圓C上的一個動點,點P在線段AM上,點N在線段CM上,且滿足| AM |
| AP |
| NP |
| AM |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| ax |
| x+b |
| 2m |
| (x+1)|x-m| |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| AE |
| AF |
| EP |
| OA |
| FO |
| OP |
| AM |
| AN |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
| ||
| 5 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com