
 ,根據點A和求出的斜率寫出直線AB的方程,然后聯立直線AB與已知直線得到關于x與y的二元一次方程組,求出方程組的解即可得到點B的坐標.
,根據點A和求出的斜率寫出直線AB的方程,然后聯立直線AB與已知直線得到關于x與y的二元一次方程組,求出方程組的解即可得到點B的坐標.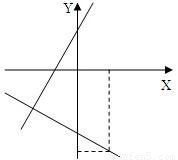 解:如圖.易知當AB的連線與已知直線垂直時,AB的長度最短.
解:如圖.易知當AB的連線與已知直線垂直時,AB的長度最短.
 (x-2),⇒x+2y+8=0,
(x-2),⇒x+2y+8=0,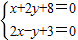 ⇒
⇒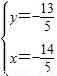 ,
,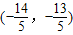 .
.

科目:高中數學 來源:2011-2012學年浙江省溫州市十校聯合體高二(上)期中數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com