
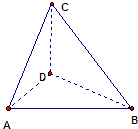
 設Rt△ABC斜邊AB上的高是CD,AC=BC=2,沿高CD作折痕將之折成直二面角A-CD-B(如圖)那么得到二面角C-AB-D的余弦值等于( )
設Rt△ABC斜邊AB上的高是CD,AC=BC=2,沿高CD作折痕將之折成直二面角A-CD-B(如圖)那么得到二面角C-AB-D的余弦值等于( )| 2 |
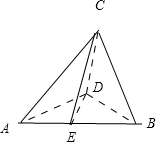
| ||||
| 2 |
| CD2+DE2 |
| 2+1 |
| 3 |
| DE |
| CE |
| 1 | ||
|
| ||
| 3 |


科目:高中數學 來源: 題型:
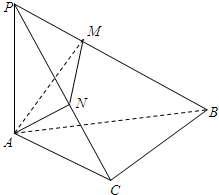 如圖所示,在斜邊為AB的Rt△ABC中,過A作PA⊥平面ABC,AM⊥PB于M,
如圖所示,在斜邊為AB的Rt△ABC中,過A作PA⊥平面ABC,AM⊥PB于M,查看答案和解析>>
科目:高中數學 來源:設計必修五數學蘇教版 蘇教版 題型:044
如圖所示,在Rt△ABC中,∠A、∠B、∠C的對邊分別為a、b、c,斜邊c是△ABC外接圓的直徑(設Rt△ABC外接圓的半徑為R),則![]() ,這個結論對鈍角三角形、銳角三角形是否也成立呢?你能否結合圓形及初中所學幾何知識作出相應的解釋?
,這個結論對鈍角三角形、銳角三角形是否也成立呢?你能否結合圓形及初中所學幾何知識作出相應的解釋?

查看答案和解析>>
科目:高中數學 來源:浙江省東陽中學2012屆高三上學期期中考試數學理科試題 題型:013
設Rt△ABC的三邊分別為a,b,c,其中c為斜邊,直線ax+by+c=0與圓cos2![]() ·x2+cos2
·x2+cos2![]() ·y2=1,(
·y2=1,(![]() 為常數,
為常數,![]() ∈(0,
∈(0,![]() )交于M、N兩點,則|MN|=
)交于M、N兩點,則|MN|=
sin![]()
2sin![]()
tan![]()
2tan![]()
查看答案和解析>>
科目:高中數學 來源:2011-2012學年浙江省高三上學期期中考試理科數學 題型:選擇題
設Rt△ABC的三邊分別為a,b,c,其中c為斜邊,m]直線ax+by+c=0與圓 ,(
,(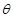 為常數,
為常數,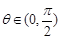 )交于
)交于 兩點,則
兩點,則
A.sinθ B.2sinθ C.tanθ D.2tanθ
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com