
某同學用《幾何畫板》研究拋物線的性質:打開《幾何畫板》軟件,繪制某拋物線 ,在拋物線上任意畫一個點
,在拋物線上任意畫一個點 ,度量點
,度量點 的坐標
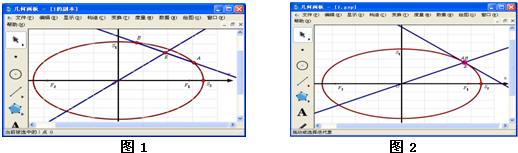
的坐標 ,如圖.
,如圖.

(Ⅰ)拖動點 ,發現當
,發現當 時,
時, ,試求拋物線
,試求拋物線 的方程;
的方程;
(Ⅱ)設拋物線 的頂點為
的頂點為 ,焦點為
,焦點為 ,構造直線
,構造直線 交拋物線
交拋物線 于不同兩點
于不同兩點 、
、 ,構造直線
,構造直線 、
、 分別交準線于
分別交準線于 、
、 兩點,構造直線
兩點,構造直線 、
、 .經觀察得:沿著拋物線
.經觀察得:沿著拋物線 ,無論怎樣拖動點
,無論怎樣拖動點 ,恒有
,恒有
 .請你證明這一結論.
.請你證明這一結論.
(Ⅲ)為進一步研究該拋物線 的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點
的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點 ”改變為其它“定點
”改變為其它“定點
 ”,其余條件不變,發現“
”,其余條件不變,發現“ 與
與 不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
 ”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
(Ⅰ)
(Ⅱ)設出直線方程,點的坐標,聯立方程組證明
 ,所以
,所以

(Ⅲ)設拋物線 的頂點為
的頂點為 ,定點
,定點 ,過點
,過點 的直線
的直線 與拋物線
與拋物線 相交于
相交于 、
、 兩點,直線
兩點,直線 、
、 分別交直線
分別交直線 于
于 、
、 兩點,則
兩點,則

【解析】
試題分析:解法一:(Ⅰ)把 ,
, 代入
代入 ,得
,得 ,
2分
,
2分
所以 ,
3分
,
3分
因此,拋物線 的方程
的方程 .
4分
.
4分
(Ⅱ)因為拋物線 的焦點為
的焦點為 ,設
,設 ,
,
依題意可設直線 ,
,
由 得
得 ,則
,則 ① 6分
① 6分
又因為 ,
, ,所以
,所以 ,
, ,
,
所以 ,
, , 7分
, 7分
又因為 8分
8分



 , ②
, ②
把①代入②,得 , 10分
, 10分
即 ,
,
所以
 ,
,
又因為 、
、 、
、 、
、 四點不共線,所以
四點不共線,所以
 . 11分
. 11分
(Ⅲ)設拋物線 的頂點為
的頂點為 ,定點
,定點 ,過點
,過點 的直線
的直線 與拋物線
與拋物線 相交于
相交于 、
、 兩點,直線
兩點,直線 、
、 分別交直線
分別交直線 于
于 、
、 兩點,則
兩點,則
 . 14分
. 14分
解法二:(Ⅰ)同解法一.
(Ⅱ)因為拋物線 的焦點為
的焦點為 ,設
,設 , 5分
, 5分
依題意,可設直線 ,
,
由 得
得 ,
,
則
所以 7分
7分
又因為 ,
, ,
,
所以 ,
, , 10分
, 10分
所以 ,
, ,
,
又因為 、
、 、
、 、
、 四點不共線,所以
四點不共線,所以
 .
11分
.
11分
(Ⅲ)同解法一. 14分
解法三:(Ⅰ)同解法一.
(Ⅱ)因為拋物線 的焦點為
的焦點為 ,設
,設 ,
,
依題意,設直線 ,
,
由 得
得 ,則
,則 , 6分
, 6分
又因為 ,
, ,所以
,所以 ,
, ,
,
又因為
 , 9分
, 9分
所以 ,所以
,所以 平行于
平行于 軸;
軸;
同理可證 平行于
平行于 軸;
軸;
又因為 、
、 、
、 、
、 四點不共線,所以
四點不共線,所以
 . 11分
. 11分
(Ⅲ)同解法一. 14分
考點:本小題主要考查拋物線的標準方程、直線與圓錐曲線的位置關系.
點評:圓錐曲線問題在高考中每年必考,且一般出在壓軸題的位置上,難度較低,主要考查推理論證能力、運算求解能力,考查化歸與轉化思想、分類與整合思想、數形結合思想等。


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
某同學用《幾何畫板》研究拋物線的性質:打開《幾何畫板》軟件,繪制某拋物線![]() ,在拋物線上任意畫一個點
,在拋物線上任意畫一個點![]() ,度量點
,度量點![]() 的坐標
的坐標![]() ,如圖.
,如圖.
(Ⅰ)拖動點![]() ,發現當
,發現當![]() 時,
時,![]() ,試求拋物線
,試求拋物線![]() 的方程;
的方程;
(Ⅱ)設拋物線![]() 的頂點為
的頂點為![]() ,焦點為
,焦點為![]() ,構造直線
,構造直線![]() 交拋物線
交拋物線![]() 于不同兩點
于不同兩點![]() 、
、![]() ,構造直線
,構造直線![]() 、
、![]() 分別交準線于
分別交準線于![]() 、
、![]() 兩點,構造直線
兩點,構造直線![]() 、
、![]() .經觀察得:沿著拋物線
.經觀察得:沿著拋物線![]() ,無論怎樣拖動點
,無論怎樣拖動點![]() ,恒有
,恒有![]()
![]() .請你證明這一結論.
.請你證明這一結論.
(Ⅲ)為進一步研究該拋物線![]() 的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點
的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點![]() ”改變為其它“定點
”改變為其它“定點![]()
![]() ”,其余條件不變,發現“
”,其余條件不變,發現“![]() 與
與![]() 不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“![]()
![]() ”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
”成立?如果可以,請寫出相應的正確命題;否則,說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
某同學用《幾何畫板》研究拋物線的性質:打開《幾何畫板》軟件,繪制某拋物線![]() ,在拋物線上任意畫一個點
,在拋物線上任意畫一個點![]() ,度量點
,度量點![]() 的坐標
的坐標![]() ,如圖.
,如圖.
(Ⅰ)拖動點![]() ,發現當
,發現當![]() 時,
時,![]() ,試求拋物線
,試求拋物線![]() 的方程;
的方程;
(Ⅱ)設拋物線![]() 的頂點為
的頂點為![]() ,焦點為
,焦點為![]() ,構造直線
,構造直線![]() 交拋物線
交拋物線![]() 于不同兩點
于不同兩點![]() 、
、![]() ,構造直線
,構造直線![]() 、
、![]() 分別交準線于
分別交準線于![]() 、
、![]() 兩點,構造直線
兩點,構造直線![]() 、
、![]() .經觀察得:沿著拋物線
.經觀察得:沿著拋物線![]() ,無論怎樣拖動點
,無論怎樣拖動點![]() ,恒有
,恒有![]()
![]() .請你證明這一結論.
.請你證明這一結論.
(Ⅲ)為進一步研究該拋物線![]() 的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點
的性質,某同學進行了下面的嘗試:在(Ⅱ)中,把“焦點![]() ”改變為其它“定點
”改變為其它“定點![]()
![]() ”,其余條件不變,發現“
”,其余條件不變,發現“![]() 與
與![]() 不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“
不再平行”.是否可以適當更改(Ⅱ)中的其它條件,使得仍有“![]()
![]() ”成立?如果可以,請寫出相應的正確命題;否則,說明理由.
”成立?如果可以,請寫出相應的正確命題;否則,說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com