
中日“釣魚島爭端”問題越來越引起社會關注,我校對高一600名學生進行了一次“釣魚島”知識測試,并從中抽取了部分學生的成績(滿分100分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖.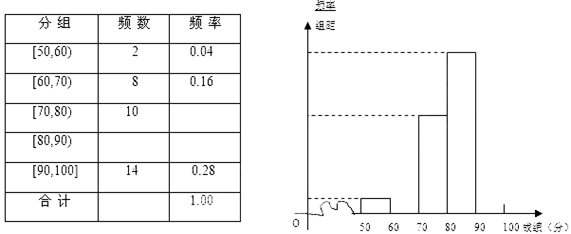
(1)填寫答題卡頻率分布表中的空格,補全頻率分布直方圖,并標出每個小矩形對應的縱軸數據;
(2)試估計該年段成績在 段的有多少人;
段的有多少人;
(3)請你估算該年級的平均分.
 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:解答題
學校為了預防甲流感,每天上午都要對同學進行體溫抽查。某一天,隨機抽取甲、乙兩個班級各10名同學,測量他們的體溫如圖:(單位0.1℃)
(1)哪個班所選取的這10名同學的平均體溫高?
(2)一般 ℃為低熱,
℃為低熱, ℃為中等熱,
℃為中等熱, ℃為高熱。按此規定,記事件A為“從甲班發熱的同學中任選兩人,有中等熱的同學”,記事件B為“從乙班發熱的同學中任選兩人,有中等熱的同學”,分別求事件A和事件B的概率.
℃為高熱。按此規定,記事件A為“從甲班發熱的同學中任選兩人,有中等熱的同學”,記事件B為“從乙班發熱的同學中任選兩人,有中等熱的同學”,分別求事件A和事件B的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知某池塘養殖著鯉魚和鯽魚,為了估計這兩種魚的數量,養殖者從池塘中捕出兩種魚各 只,給每只魚做上不影響其存活的標記,然后放回池塘,待完全混合后,再每次從池塘中隨機的捕出
只,給每只魚做上不影響其存活的標記,然后放回池塘,待完全混合后,再每次從池塘中隨機的捕出 只魚,記錄下其中有記號的魚的數目,立即放回池塘中。這樣的記錄做了
只魚,記錄下其中有記號的魚的數目,立即放回池塘中。這樣的記錄做了 次,并將記錄獲取的數據做成以下的莖葉圖。
次,并將記錄獲取的數據做成以下的莖葉圖。
(Ⅰ)根據莖葉圖計算有記號的鯉魚和鯽魚數目的平均數,并估計池塘中的鯉魚和鯽魚的數量;
(Ⅱ)為了估計池塘中魚的總重量,現從中按照(Ⅰ)的比例對 條魚進行稱重,據稱重魚的重量介于
條魚進行稱重,據稱重魚的重量介于 (單位:千克)之間,將測量結果按如下方式分成九組:第一組
(單位:千克)之間,將測量結果按如下方式分成九組:第一組 、第二組
、第二組 ;……,第九組
;……,第九組 。右圖是按上述分組方法得到的頻率分布直方圖的一部分。
。右圖是按上述分組方法得到的頻率分布直方圖的一部分。
①估計池塘中魚的重量在 千克以上(含
千克以上(含 千克)的條數;
千克)的條數;
②若第二組、第三組、第四組魚的條數依次成公差為 的等差數列,請將頻率分布直方圖補充完整;
的等差數列,請將頻率分布直方圖補充完整;
③在②的條件下估計池塘中魚的重量的眾數、中位數及估計池塘中魚的總重量;
(Ⅲ)假設隨機地從池塘逐只有放回的捕出 只魚中出現鯉魚的次數為
只魚中出現鯉魚的次數為 ,求
,求 的數學期望。
的數學期望。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品的廣告費支出 與銷售額
與銷售額 (單位:萬元)之間有如下對應數據:
(單位:萬元)之間有如下對應數據:
 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |

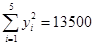
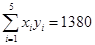 ,
,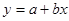 ,其中
,其中 )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
有甲、乙兩個班級進行數學考試,按照大于或等于85分為優秀,85分以下為非優秀統計成績后,得到如下的 列聯表:已知從全部210人中隨機抽取1人為優秀的概率為
列聯表:已知從全部210人中隨機抽取1人為優秀的概率為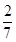 .
.
| | 優秀 | 非優秀 | 總計 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合計 | | | 210 |
 列聯表,并判斷若按99%的可靠性要求,能否認為“成績與班級有關”;
列聯表,并判斷若按99%的可靠性要求,能否認為“成績與班級有關”;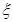 ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求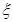 的分布列及數學期望
的分布列及數學期望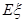 .
.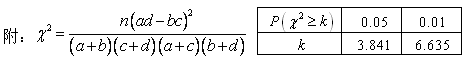
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在生產過程中,測得纖維產品的纖度(表示纖維粗細的一種量)共有100個數據,將數據分組如表:
| 分組 | 頻數 |
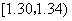 | 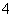 |
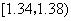 |  |
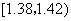 |  |
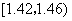 | 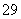 |
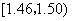 |  |
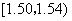 |  |
| 合計 |  |
 中的概率及纖度小于
中的概率及纖度小于 的概率是多少?
的概率是多少?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某班同學利用寒假在5個居民小區內選擇兩個小區逐戶進行一次“低碳生活習慣”的調查,以計算每戶每月的碳排放量.若月排放量符合低碳標準的稱為“低碳族”,否則稱為“非低碳族”.若小區內有至少 的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區”.已知備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
的住戶屬于“低碳族”,則稱這個小區為“低碳小區”,否則稱為“非低碳小區”.已知備選的5個居民小區中有三個非低碳小區,兩個低碳小區.
(1)求所選的兩個小區恰有一個為“非低碳小區”的概率;
(2)假定選擇的“非低碳小區”為小區 ,調查顯示其“低碳族”的比例為
,調查顯示其“低碳族”的比例為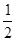 ,數據如圖1所示,經過同學們的大力宣傳,三個月后,又進行了一次調查,數據如圖2所示,問這時小區
,數據如圖1所示,經過同學們的大力宣傳,三個月后,又進行了一次調查,數據如圖2所示,問這時小區 是否達到“低碳小區”的標準?
是否達到“低碳小區”的標準?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解目前老年人居家養老還是在敬老院養老的意向,共調查了50名老年人,其中男性明確表示去敬老院養老的有5人,女性明確表示居家養老的有10人,已知在全部50人中隨機地抽取1人明確表示居家養老的概率為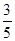 。
。
(1)請根據上述數據建立一個2×2列聯表;(2)居家養老是否與性別有關?請說明理由。
參考數據:
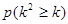 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
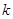 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某次測驗中,有6位同學的平均成績為75分.用xn表示編號為n(n=1,2, ,6)的同學所得成績,且前5位同學的成績如下:
| 編號n | 1 | 2 | 3 | 4 | 5 |
| 成績xn | 70 | 76 | 72 | 70 | 72 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com