
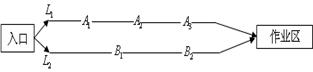
某煤礦發生透水事故時,作業區有若干人員被困.救援隊從入口進入之后有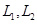 兩條巷道通往作業區(如下圖),
兩條巷道通往作業區(如下圖),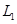 巷道有
巷道有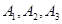 三個易堵塞點,各點被堵塞的概率都是
三個易堵塞點,各點被堵塞的概率都是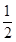 ;
;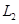 巷道有
巷道有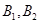 兩個易堵塞點,被堵塞的概率分別為
兩個易堵塞點,被堵塞的概率分別為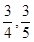 .
.
(1)求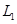 巷道中,三個易堵塞點最多有一個被堵塞的概率;
巷道中,三個易堵塞點最多有一個被堵塞的概率;
(2)若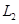 巷道中堵塞點個數為
巷道中堵塞點個數為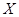 ,求
,求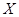 的分布列及數學期望
的分布列及數學期望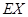 ,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
,并按照"平均堵塞點少的巷道是較好的搶險路線"的標準,請你幫助救援隊選擇一條搶險路線,并說明理由.
(1)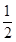 ;(2)分布列詳見解析;
;(2)分布列詳見解析; ;選擇
;選擇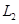 巷道為搶險路線為好.
巷道為搶險路線為好.
解析試題分析:(1)利用互獨立事件的概率計算公式即可得出;
科目:高中數學
來源:
題型:解答題
為了解七班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
科目:高中數學
來源:
題型:解答題
設每個工作日甲、乙、丙、丁4人需使用某種設備的概率分別是0.6, 0.5,0.5,0.4,各人是否使用設備相互獨立,
科目:高中數學
來源:
題型:解答題
(本小題滿分12分)
科目:高中數學
來源:
題型:解答題
甲乙兩人進行圍棋比賽,約定先連勝兩局者直接贏得比賽,若賽完5局仍未出現連勝,則判定獲勝局數多者贏得比賽,假設每局甲獲勝的概率為
科目:高中數學
來源:
題型:解答題
某電視臺的一個智力游戲節目中,有一道將中國四大名著《三國演義》、《水滸傳》、《西游記》、《紅樓夢》與它們的作者連線的題目,每本名著只能與一名作者連線,每名作者也只能與一本名著連線,每連對一個得2分,連錯得-1分,某觀眾只知道《三國演義》的作者是羅貫中,其他不知道隨意連線,將他的得分記作ξ.
科目:高中數學
來源:
題型:解答題
如圖,一半徑為
科目:高中數學
來源:
題型:解答題
前不久,社科院發布了2013年度“全國城市居民幸福排行榜”,北京市成為本年度最“幸福城”.隨后,某師大附中學生會組織部分同學,用“10分制”隨機調查“陽光”社區人們的幸福度.現從調查人群中隨機抽取16名,如圖所示的莖葉圖記錄了他們的幸福度分數(以小數點前的一位數字為莖,小數點后一位為葉):
科目:高中數學
來源:
題型:解答題
甲、乙兩名運動員參加“選拔測試賽”,在相同條件下,兩人5次測試的成績(單位:分)記錄如下:
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
(2)寫出隨機變量X的所有可能取值,然后計算相應的概率,列表即得分布列,由數學期望公式計算期望的大小.
比較走兩條路的數學期望的大小,即可得出要選擇的路線.
(1)設 巷道中,三個易堵塞點最多有一個被堵塞
巷道中,三個易堵塞點最多有一個被堵塞 為事件
為事件
則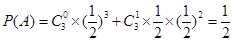 4分
4分
(2)依題意,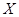 的可能取值為0,1,2
的可能取值為0,1,2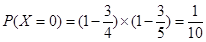
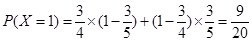
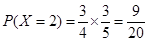
所以,隨機變量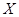 的分布列為:
的分布列為: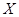
0 1 2 
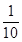
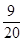
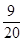
 8分
8分
(方法一)設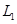 巷道中堵塞點個數為
巷道中堵塞點個數為 ,則
,則 的可能取值為0,1,2,3
的可能取值為0,1,2,3
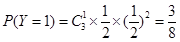
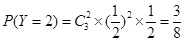
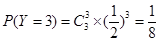
所以,隨機變量 的分布列為:
的分布列為:
0 1 2 3 

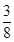
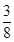



0系列答案
智多星創新達標考試卷系列答案
文言文完全解讀系列答案
初中文言文譯注及賞析系列答案
初中文言文全解一本通系列答案
超級教輔全能100分系列答案

黃岡小狀元數學詳解系列答案
高分密碼培優必練系列答案
本真語文踩點奪分系列答案
喜愛打籃球
不喜愛打籃球
合計
男生
5
女生
10
合計
50
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為 .(12分)
.(12分)
(1)請將上面的列聯表補充完整(不用寫計算過程);
(2)能否在犯錯誤的概率不超過0.005的前提下認為喜愛打籃球與性別有關?說明你的理由;
(3)現從女生中抽取2人進一步調查,設其中喜愛打籃球的女生人數為 ,求
,求 的分布列與期望.
的分布列與期望.
下面的臨界值表供參考:
0.15
0.10
0.05[
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
(參考公式: ,其中
,其中 )
)
(1)求同一工作日至少3人需使用設備的概率;
(2)實驗室計劃購買k臺設備供甲、乙、丙、丁使用,若要求“同一工作日需使用設備的人數大于k”的概率小于0.1,求k的最小值.
乒乓球臺面被球網分成甲、乙兩部分,如圖,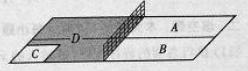 甲上有兩個不相交的區域
甲上有兩個不相交的區域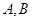 ,乙被劃分為兩個不相交的區域
,乙被劃分為兩個不相交的區域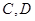 .某次測試要求隊員接到落點在甲上的來球后向乙回球.規定:回球一次,落點在
.某次測試要求隊員接到落點在甲上的來球后向乙回球.規定:回球一次,落點在 上記3分,在
上記3分,在 上記1分,其它情況記0分.對落點在
上記1分,其它情況記0分.對落點在 上的來球,隊員小明回球的落點在
上的來球,隊員小明回球的落點在 上的概率為
上的概率為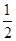 ,在
,在 上的概率為
上的概率為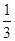 ;對落點在
;對落點在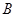 上的來球,小明回球的落點在
上的來球,小明回球的落點在 上的概率為
上的概率為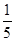 ,在
,在 上的概率為
上的概率為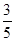 .假設共有兩次來球且落在
.假設共有兩次來球且落在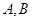 上各一次,小明的兩次回球互不影響.求:
上各一次,小明的兩次回球互不影響.求:
(Ⅰ)小明的兩次回球的落點中恰有一次的落點在乙上的概率;
(Ⅱ)兩次回球結束后,小明得分之和 的分布列與數學期望.
的分布列與數學期望.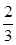 ,乙獲勝的概率為
,乙獲勝的概率為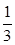 ,各局比賽結果相互獨立.
,各局比賽結果相互獨立.
求甲在4局以內(含4局)贏得比賽的概率;
記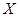 為比賽決出勝負時的總局數,求
為比賽決出勝負時的總局數,求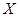 的分布列和均值(數學期望).
的分布列和均值(數學期望).
(1)求該觀眾得分ξ為負數的概率;
(2)求ξ的分布列.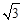 的圓形靶內有一個半徑為
的圓形靶內有一個半徑為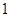 的同心圓,將大圓分成兩
的同心圓,將大圓分成兩
部分,小圓內部區域記為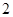 環,圓環區域記為
環,圓環區域記為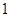 環,某同學向該靶投擲
環,某同學向該靶投擲 枚飛鏢,每次
枚飛鏢,每次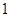 枚. 假設他每次必
枚. 假設他每次必
定會中靶,且投中靶內各點是隨機的.
(1)求該同學在一次投擲中獲得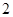 環的概率;
環的概率;
(2)設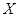 表示該同學在
表示該同學在 次投擲中獲得的環數,求
次投擲中獲得的環數,求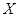 的分布列及數學期望.
的分布列及數學期望.
指出這組數據的眾數和中位數;
若幸福度不低于9.5分,則稱該人的幸福度為“極幸福”.求從這16人中隨機選取3人,至多有1人是“極幸福”的概率;
以這16人的樣本數據來估計整個社區的總體數據,若從該社區(人數很多)人選3人,記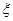 表示抽到“極幸福”的人數,求
表示抽到“極幸福”的人數,求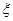 的分布列及數學期望.
的分布列及數學期望.
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用莖葉圖表示這兩組數據;.
(2)現要從中選派一名運動員參加比賽,你認為選派誰參賽更好?說明理由(不用計算);
(3)若將頻率視為概率,對運動員甲在今后三次測試成績進行預測,記這三次成績高于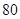 分的次數為
分的次數為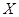 ,求
,求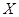 的分布列和數學期望
的分布列和數學期望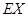 ..
..
版權聲明:本站所有文章,圖片來源于網絡,著作權及版權歸原作者所有,轉載無意侵犯版權,如有侵權,請作者速來函告知,我們將盡快處理,聯系qq:3310059649。
ICP備案序號: 滬ICP備07509807號-10 鄂公網安備42018502000812號