
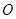 ������(bi��o)ԭ�c(di��n)����(d��ng)�c(di��n)
������(bi��o)ԭ�c(di��n)����(d��ng)�c(di��n)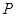 �c�ɂ�(g��)���c(di��n)
�c�ɂ�(g��)���c(di��n)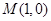 ��
��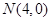 �ľ��x֮�Ȟ�
�ľ��x֮�Ȟ�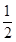 ��
��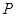 ��܉�E
��܉�E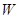 �ķ��̣�
�ķ��̣�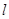 ��
��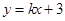 �c����
�c����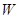 ����
����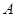 ��
��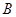 ���c(di��n)��������
���c(di��n)��������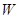 ���Ƿ����һ�c(di��n)
���Ƿ����һ�c(di��n)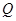 ��ʹ��
��ʹ��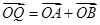 �������ڣ�����˕r(sh��)ֱ��
�������ڣ�����˕r(sh��)ֱ��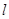 ��б�ʣ��������ڣ��f�����ɣ�
��б�ʣ��������ڣ��f�����ɣ�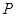 ������(bi��o)��
������(bi��o)��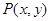 �����}�⣬
�����}�⣬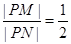 �� ������1��
�� ������1��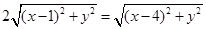 �� ����������������3��
�� ����������������3��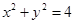 ��
��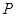 ��܉�E
��܉�E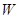 �ķ��̞�
�ķ��̞�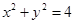 �� ����������������5��
�� ����������������5��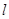 ��
��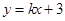 �c����
�c����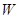 �ཻ��
�ཻ��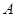 ��
��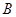 ���c(di��n)��
���c(di��n)��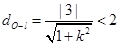 ��
��  ��
�� �� ����������������7��
�� ����������������7��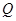 ��ʹ��
��ʹ��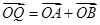 �� ����������������8��
�� ����������������8��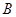 �ڈA�ϣ���
�ڈA�ϣ���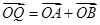 ��
��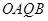 ������
������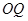 �c
�c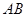 ���ഹֱ��ƽ�֣� ��������9��
���ഹֱ��ƽ�֣� ��������9��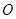 ��ֱ��
��ֱ��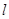 ��
��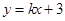 �ľ��x��
�ľ��x�� ����������10��
����������10��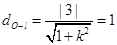 �����
�����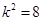 ��
�� 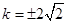 ����(j��ng)�(y��n)�C�M��l��������������������12��
����(j��ng)�(y��n)�C�M��l��������������������12��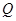 ��ʹ��
��ʹ��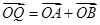 �� ����������������13��
�� ����������������13��

 �W(xu��)����܇�����������������쾚ϵ�д�
�W(xu��)����܇�����������������쾚ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
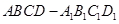 �У�
��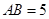 ��
��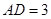 ��
��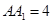 ��
��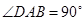 ��
��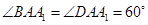 ��
��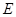 ��
��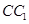 �����c(di��n)���O(sh��)
�����c(di��n)���O(sh��)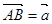 ��
��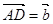 ��
��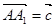 ��
��
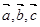 ��ʾ
��ʾ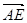 ��
��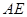 ���L��
���L���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
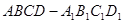 �У�
��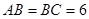 �����^
�����^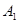 ��
��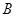 ��
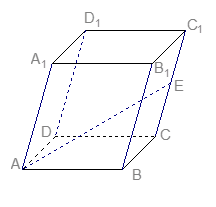
��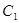 ���c(di��n)��ƽ���ȥ�L���w��һ��(g��)�Ǻ�������D�Ď��w�����@���w���w�e��120��
���c(di��n)��ƽ���ȥ�L���w��һ��(g��)�Ǻ�������D�Ď��w�����@���w���w�e��120��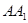 ���L��
���L��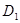 ��ƽ��
��ƽ��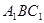 �ľ��x��
�ľ��x��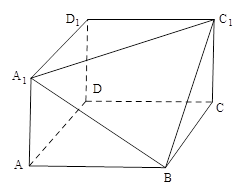
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
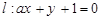 �ľ��x��ȣ��ta��ֵ�� ��
�ľ��x��ȣ��ta��ֵ�� ��A��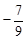 | B��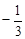 | C��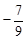 �� ��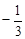 | D��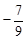 ��1 ��1 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
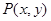 ��ֱ��
��ֱ��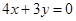 �ϣ��ҝM��
�ϣ��ҝM��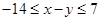 ���t�c(di��n)P������(bi��o)ԭ�c(di��n)���x��ȡֵ������( )
���t�c(di��n)P������(bi��o)ԭ�c(di��n)���x��ȡֵ������( ) | A��[0��5]������ | B��[0��10]�������� | C��[5��10]������ | D��[5��15] |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
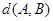 =( )
=( )| A��3 | B��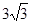 | C��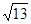 | D��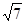 |
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com