
設函數 定義域為
定義域為 .
.
(1)若 ,求實數
,求實數 的取值范圍;
的取值范圍;
(2)若 在
在 上恒成立,求實數
上恒成立,求實數 的取值范圍.
的取值范圍.
(1)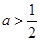 ,(2)
,(2)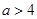 .
.
解析試題分析:(1)因為 ,所以
,所以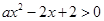 在
在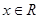 上恒成立. ① 當
上恒成立. ① 當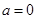 時,由
時,由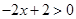 ,得
,得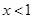 ,不成立,舍去,② 當
,不成立,舍去,② 當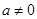 時,由
時,由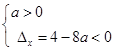 ,得
,得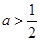 ,綜上所述,實數
,綜上所述,實數 的取值范圍是
的取值范圍是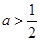 .(2))恒成立問題一般利用變量分離法轉化為最值問題. 依題有
.(2))恒成立問題一般利用變量分離法轉化為最值問題. 依題有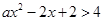 在
在 上恒成立,所以
上恒成立,所以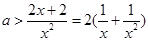 在
在 上恒成立, 令
上恒成立, 令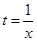 ,則由
,則由 ,得
,得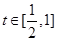 ,記
,記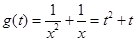 ,由于
,由于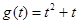 在
在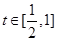 上單調遞增, 所以
上單調遞增, 所以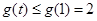 ,
, 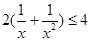
因此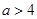
試題解析:解:(1)因為 ,所以
,所以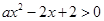 在
在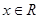 上恒成立. 2分
上恒成立. 2分
① 當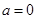 時,由
時,由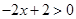 ,得
,得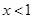 ,不成立,舍去, 4分
,不成立,舍去, 4分
② 當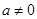 時,由
時,由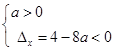 ,得
,得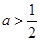 , 6分
, 6分
綜上所述,實數 的取值范圍是
的取值范圍是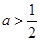 . 8分
. 8分
(2)依題有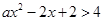 在
在 上恒成立, 10分
上恒成立, 10分
所以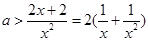 在
在 上恒成立, 12分
上恒成立, 12分
令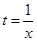 ,則由
,則由 ,得
,得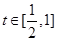 ,
,
記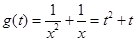 ,由于
,由于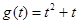 在
在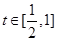 上單調遞增,
上單調遞增,
所以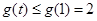 ,
, 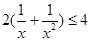
因此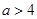 16分
16分
(使用函數在定義區間上最小值大于0求解可參照給分)
考點:不等式恒成立問題


科目:高中數學 來源: 題型:解答題
如圖,ABCD是正方形空地,邊長為30m,電源在點P處,點P到邊AD、AB距離分別為9m,3m.某廣告公司計劃在此空地上豎一塊長方形液晶廣告屏幕MNEF,MN:NE=16:9.線段MN必須過點P,端點M,N分別在邊AD,AB上,設AN=x(m),液晶廣告屏幕MNEF的面積為S(m2).
(1)用x的代數式表示AM,并寫出x的取值范圍;
(2)求S關于x的函數關系式.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某市環保部門對市中心每天環境污染情況進行調查研究,發現一天中環境污染指數 與時刻
與時刻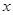 (時)的關系為
(時)的關系為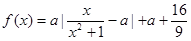 ,
, ,其中
,其中 是與氣象有關的參數,且
是與氣象有關的參數,且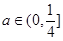 ,用每天
,用每天 的最大值作為當天的污染指數,記作
的最大值作為當天的污染指數,記作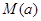 .
.
(1)令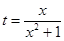 ,
, ,求
,求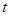 的取值范圍;
的取值范圍;
(2)按規定,每天的污染指數不得超過2,問目前市中心的污染指數是否超標?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地需要修建一條大型輸油管道通過240公里寬的沙漠地帶,該段輸油管道兩端的輸油站已建好,余下工程是在該段兩端已建好的輸油站之間鋪設輸油管道和等距離修建增壓站(又稱泵站).經預算,修建一個增壓站的工程費用為400萬元,鋪設距離為 公里的相鄰兩增壓站之間的輸油管道費用為
公里的相鄰兩增壓站之間的輸油管道費用為 萬元.設余下工程的總費用為
萬元.設余下工程的總費用為 萬元.
萬元.
(1)試將 表示成
表示成 的函數;
的函數;
(2)需要修建多少個增壓站才能使 最小,其最小值為多少?
最小,其最小值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如果n件產品中任取一件樣品是次品的概率為 ,則認為這批產品中有
,則認為這批產品中有 件次品。某企業的統計資料顯示,產品中發生次品的概率p與日產量n滿足
件次品。某企業的統計資料顯示,產品中發生次品的概率p與日產量n滿足
 ,有已知每生產一件正品可贏利a元,如果生產一件次品,非但不能贏利,還將損失
,有已知每生產一件正品可贏利a元,如果生產一件次品,非但不能贏利,還將損失 元(
元( ).
).
(1)求該企業日贏利額 的最大值;
的最大值;
(2)為保證每天的贏利額不少于日贏利額最大值的50%,試求該企業日產量的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
請你設計一個包裝盒,如圖所示, 是邊長為
是邊長為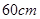 的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得
的正方形硬紙片,切去陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使得 四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒,
四個點重合于圖中的點P,正好形成一個正四棱柱形狀的包裝盒, 在
在 上是被切去的等腰直角三角形斜邊的兩個端點,設
上是被切去的等腰直角三角形斜邊的兩個端點,設 .
.
(1)若廣告商要求包裝盒側面積 最大,試問
最大,試問 應取何值?
應取何值?
(2)若廣告商要求包裝盒容積 最大,試問
最大,試問 應取何值?并求出此時包裝盒的高與底面邊長的比值.
應取何值?并求出此時包裝盒的高與底面邊長的比值.

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數
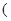 常數
常數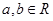 )滿足
)滿足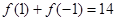 .
.
(1)求出 的值,并就常數
的值,并就常數 的不同取值討論函數
的不同取值討論函數 奇偶性;
奇偶性;
(2)若 在區間
在區間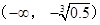 上單調遞減,求
上單調遞減,求 的最小值;
的最小值;
(3)在(2)的條件下,當 取最小值時,證明:
取最小值時,證明: 恰有一個零點
恰有一個零點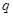 且存在遞增的正整數數列
且存在遞增的正整數數列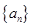 ,使得
,使得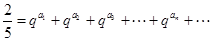 成立.
成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com