
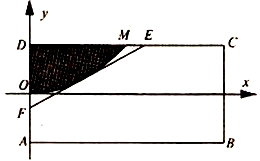
 有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,已知AB=4米,AD=2米.
有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,已知AB=4米,AD=2米.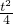
 ,求導,得,y′=
,求導,得,y′=
 ,切線EF的方程為y-m=
,切線EF的方程為y-m= (x-t)
(x-t)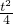 代入,得,y-
代入,得,y-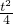 =
= (x-t)
(x-t)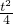 =
= (x-t)中x=0,得,y=-
(x-t)中x=0,得,y=-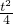

 |DE||DF|=
|DE||DF|= (1+
(1+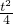 )(
)( )=
)=
 ,當t∈[0,1]時,S′△DEF<0
,當t∈[0,1]時,S′△DEF<0
 ),AF=
),AF=
 時,截去的△DEF的面積最小.
時,截去的△DEF的面積最小.

 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:高中數學 來源: 題型:
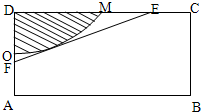 如圖,有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,若AB=1米,AD=0.5米,當沿切割線EF切割使剩余部分五邊形ABCEF的面積最大時,AF的長度為( )米.
如圖,有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,若AB=1米,AD=0.5米,當沿切割線EF切割使剩余部分五邊形ABCEF的面積最大時,AF的長度為( )米.A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,已知AB=4米,AD=2米.
有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到點D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,已知AB=4米,AD=2米.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,若AB=1米,AD=0.5米,向如何畫切割線EF可使剩余部分五邊形ABCEF的面積最大?
如圖,有一矩形鋼板ABCD缺損了一角(圖中陰影部分),邊緣線OM上每一點到D的距離都等于它到邊AB的距離.工人師傅要將缺損的一角切割下來使剩余部分成一個五邊形,若AB=1米,AD=0.5米,向如何畫切割線EF可使剩余部分五邊形ABCEF的面積最大?查看答案和解析>>
科目:高中數學 來源:河北省期末題 題型:解答題
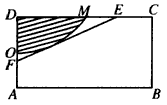
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com