Question

已知數列｛｝中，在直線y=x上，其中n=1,2,3….

(Ⅰ)令  (Ⅱ)求數列

(Ⅲ)設的前n項和,是否存在實數，使得數列為等差數列？若存在，試求出.若不存在,則說明理由。

Answer 1

解：（I）由已知得 

又

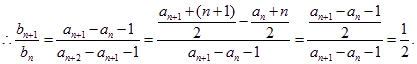
是以為首項，以為公比的等比數列.

（II）由（I）知，

將以上各式相加得：

               

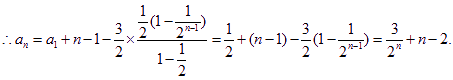
（III）解法一：

存在，使數列是等差數列.

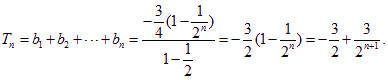
數列是等差數列的充要條件是、是常數

即

又

當且僅當，即時，數列為等差數列.

解法二：

存在，使數列是等差數列.

由（I）、（II）知，

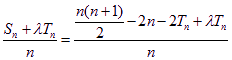
又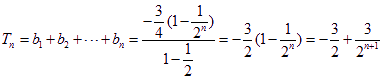

當且僅當時，數列是等差數列.

解析:

解：（I）由已知得 

又

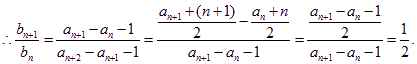
是以為首項，以為公比的等比數列.

（II）由（I）知，

將以上各式相加得：

               

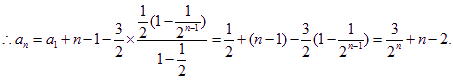
（III）解法一：

存在，使數列是等差數列.

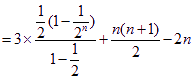
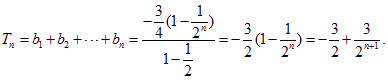
數列是等差數列的充要條件是、是常數

即

又

當且僅當，即時，數列為等差數列.

解法二：

存在，使數列是等差數列.

由（I）、（II）知，

又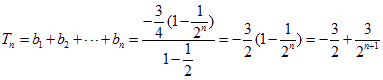

當且僅當時，數列是等差數列.