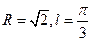設向量

,

,
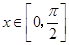
.
(1)若

,求

的值;
(2)設函數(shù)

,求
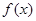
的最大值.
試題分析:(1)去除向量的包裝外衣,轉化為由三角函數(shù)值求對應的角的值;(2)去除向量的包裝外衣,轉化為形如:
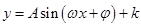
三角函數(shù)最值,但一定要關注自變量

的范圍.另外三角函數(shù)與代數(shù)函數(shù)一個很大的區(qū)別就是一般先要處理三角函數(shù)表達式,處理的結果之一就是轉化為形如:
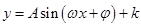
,這一點很重要.
試題解析:(1)由

得
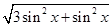
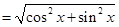
,即
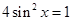
,
又∵
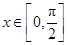
,∴

,從而

. (5分)
(2)
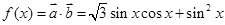
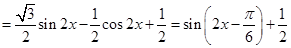
,
又∵
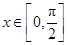
,∴
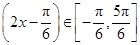
,即有

,所以
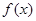
的最大值為
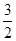
. (14分)
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知
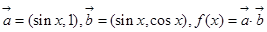
(1)若
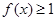
,求x的范圍;
(2)求
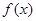
的最大值以及此時x的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在平面上,

⊥
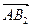
,|
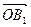
|=|

|=1,

=

+
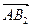
.若|

|<
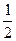
,則|

|的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
空間四邊形
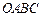
中,
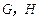
分別是
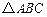
,
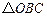
的重心,設
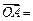
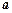
,
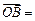
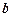
,
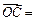
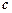
,試用向量
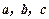
表示向量
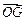
和
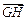
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若向量
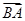
=(2,3),
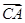
=(4,7),則

=( )
| A.(-2,-4) | B.(2,4) | C.(6,10) | D.(-6,-10) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
下列說法正確的是( )
| A.平面內(nèi)的任意兩個向量都共線 | B.空間的任意三個向量都不共面 |
| C.空間的任意兩個向量都共面 | D.空間的任意三個向量都共面 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知A、B是球心為O的球面上的兩點,在空間直角坐標系中,它們的坐標分別為O(0,0,0)、

、

,則該球的半徑R及點A、B在該球面上的最短距離
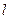
分別為
A.

B.
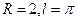
C.

D.
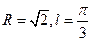
查看答案和解析>>

 ,
, ,
,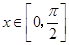 .
. ,求
,求 的值;
的值; ,求
,求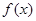 的最大值.
的最大值. 、
、 ,則該球的半徑R及點A、B在該球面上的最短距離
,則該球的半徑R及點A、B在該球面上的最短距離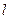 分別為
分別為 B.
B.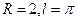 C.
C. D.
D.