
已知函數(shù)f(x)=ax+x2-xlna(a>0,a≠1).
(1)當a>1時,求證:函數(shù)f(x)在(0,+∞)上單調(diào)遞增;
(2)若函數(shù)y=|f(x)-t|-1有三個零點,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,試求a的取值范圍.
(1)見解析(2)t=2(3)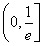 ∪[e,+∞)
∪[e,+∞)
【解析】審題引導:本題考查函數(shù)與導數(shù)的綜合性質(zhì),函數(shù)模型并不復雜,(1)(2)兩問是很常規(guī)的,考查利用導數(shù)證明單調(diào)性,考查函數(shù)與方程的零點問題.第(3)問要將“若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1”轉(zhuǎn)化成|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1成立,最后仍然是求值域問題,但在求值域過程中,問題設計比較巧妙,因為在過程中還要構造函數(shù)研究單調(diào)性來確定導函數(shù)的正負.
規(guī)范解答:(1)證明:f′(x)=axlna+2x-lna=2x+(ax-1)·lna.(2分)
由于a>1,故當x∈(0,+∞)時,lna>0,ax-1>0,所以f′(x)>0.
故函數(shù)f(x)在(0,+∞)上單調(diào)遞增.(4分)
(2)【解析】
當a>0,a≠1時,因為f′(0)=0,且f′(x)在R上單調(diào)遞增,故f′(x)=0有唯一解x=0.(6分)所以x、f′(x)、f(x)的變化情況如下表所示:
x | (-∞,0) | 0 | (0,+∞) |
f′(x) | - | 0 | + |
f(x) | ? | 極小值 | ? |
又函數(shù)y=|f(x)-t|-1有三個零點,所以方程f(x)=t±1有三個根,而t+1>t-1,所以t-1=f(x)min=f(0)=1,解得t=2.(10分)
(3)【解析】
因為存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,所以當x∈[-1,1]時,|f(x)max-f(x)min|=f(x)max-f(x)min≥e-1.(12分)
由(2)知,f(x)在[-1,0]上遞減,在[0,1]上遞增,所以當x∈[-1,1]時,f(x)min=f(0)=1,f(x)max=max{f(-1),f(1)}.
而f(1)-f(-1)=(a+1-lna)-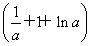 =a-
=a-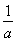 -2lna,
-2lna,
記g(t)=t- -2lnt(t>0),因為g′(t)=1+
-2lnt(t>0),因為g′(t)=1+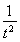 -
-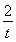 =
= ≥0(當且僅當t=1時取等號),
≥0(當且僅當t=1時取等號),
所以g(t)=t-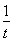 -2lnt在t∈(0,+∞)上單調(diào)遞增,而g(1)=0,
-2lnt在t∈(0,+∞)上單調(diào)遞增,而g(1)=0,
所以當t>1時,g(t)>0;當0<t<1時,g(t)<0,
也就是當a>1時,f(1)>f(-1);當0<a<1時,f(1)<f(-1).(14分)
①當a>1時,由f(1)-f(0)≥e-1?a-lna≥e-1?a≥e,
②當0<a<1時,由f(-1)-f(0)≥e-1?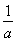 +lna≥e-1?0<a≤
+lna≥e-1?0<a≤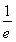 ,
,
綜上知,所求a的取值范圍為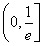 ∪[e,+∞).(16分)
∪[e,+∞).(16分)


科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第4課時練習卷(解析版) 題型:解答題
已知奇函數(shù)f(x)的定義域為[-2,2],且在區(qū)間[-2,0]內(nèi)遞減,若f(1-m)+f(1-m2)<0,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第1課時練習卷(解析版) 題型:解答題
判斷下列對應是否是從集合A到集合B的函數(shù).
(1) A=B=N*,對應法則f:x→y=|x-3|,x∈A,y∈B;
(2) A=[0,+∞),B=R,對應法則f:x→y,這里y2=x,x∈A,y∈B;
(3) A=[1,8],B=[1,3],對應法則f:x→y,這里y3=x,x∈A,y∈B;
(4) A={(x,y)|x、y∈R},B=R,對應法則:對任意(x,y)∈A,(x,y)→z=x+3y,z∈B.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第14課時練習卷(解析版) 題型:填空題
若奇函數(shù)f(x)與偶函數(shù)g(x)滿足f(x)+g(x)=2x,則函數(shù)g(x)的最小值是________.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第14課時練習卷(解析版) 題型:填空題
關于函數(shù)f(x)=lg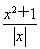 (x>0,x∈R),下列命題正確的是________.(填序號)
(x>0,x∈R),下列命題正確的是________.(填序號)
①函數(shù)y=f(x)的圖象關于y軸對稱;
②在區(qū)間(-∞,0)上,函數(shù)y=f(x)是減函數(shù);
③函數(shù)y=f(x)的最小值為lg2;
④在區(qū)間(1,+∞)上,函數(shù)y=f(x)是增函數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第13課時練習卷(解析版) 題型:解答題
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發(fā)建設,陰影部分為一公共設施建設不能開發(fā),且要求用欄柵隔開(欄柵要求在一直線上),公共設施邊界為曲線f(x)=1-ax2(a>0)的一部分,欄柵與矩形區(qū)域的邊界交于點M、N,交曲線于點P,設P(t,f(t)).
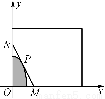
(1)將△OMN(O為坐標原點)的面積S表示成t的函數(shù)S(t);
(2)若在t=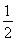 處,S(t)取得最小值,求此時a的值及S(t)的最小值.
處,S(t)取得最小值,求此時a的值及S(t)的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第13課時練習卷(解析版) 題型:填空題
某商品在近30天內(nèi)每件的銷售價格P(元)與時間t(天)的函數(shù)關系為P=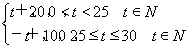 且該商品的日銷售量Q與時間t(天)的函數(shù)關系為Q=-t+40(0<t≤30,t∈N),則這種商品日銷量金額最大的一天是30天中的第________天.
且該商品的日銷售量Q與時間t(天)的函數(shù)關系為Q=-t+40(0<t≤30,t∈N),則這種商品日銷量金額最大的一天是30天中的第________天.
查看答案和解析>>
科目:高中數(shù)學 來源:2013-2014學年高考數(shù)學總復習考點引領+技巧點撥第二章第11課時練習卷(解析版) 題型:填空題
一個物體的運動方程為s=1-t+t2,其中s的單位是m,t的單位是s,那么物體在3s末的瞬時速度是_______m/s.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com