
��֪���A= ��һ��(g��)��������ֵ1����������
��һ��(g��)��������ֵ1���������� .
.
(��) ����A��
(��) �����B= ����ֱ��
����ֱ�� ���ھ��A�����ھ��B�Č�(du��)��(y��ng)׃�Q�����µ���ķ���.
���ھ��A�����ھ��B�Č�(du��)��(y��ng)׃�Q�����µ���ķ���.
��1��A=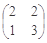 .��2��
.��2��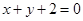
����ԇ�}������(��)����֪��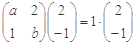 ������
������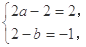 2��
2��
���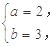 ��A=
��A=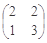 . ����������������������������������������3��
. ����������������������������������������3��
(��) BA=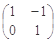
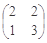 =
=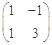 ����?y��n)���?i>BA����(du��)��(y��ng)�ľ���׃�Q��ֱ��׃��ֱ�������c(di��n)�������Կ�ȡֱ��
����?y��n)���?i>BA����(du��)��(y��ng)�ľ���׃�Q��ֱ��׃��ֱ�������c(di��n)�������Կ�ȡֱ�� �ϵă��c(di��n)��0��1������-1��2���� 4��
�ϵă��c(di��n)��0��1������-1��2���� 4��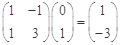 ��
��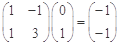 ���ɵã���0��1������-1��2���ھ��A����(du��)��(y��ng)�ľ���׃�Q�µ������c(di��n)��1��-3������-1��-1�� 6��
���ɵã���0��1������-1��2���ھ��A����(du��)��(y��ng)�ľ���׃�Q�µ������c(di��n)��1��-3������-1��-1�� 6��
�Ķ�ֱ�� �ھ��BA����(du��)��(y��ng)�ľ���׃�Q�µ���ķ��̞�
�ھ��BA����(du��)��(y��ng)�ľ���׃�Q�µ���ķ��̞�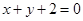 . 7��
. 7��
���c(di��n)����ꇵĸ����׃�Q
�c(di��n)�u(p��ng)����Ҫ�ǿ����˾�ꇵ�Ӌ(j��)���Լ�׃�Q���\(y��n)�ã����ڻ��A(ch��)�}��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
A��
| ||
| B��2 | ||
C��-
| ||
| D��-2 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�����A������ֵ��1=2,��2=-1,��������(du��)��(y��ng)�����������քe��e1=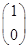 ��e2=
��e2=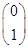 .
.
(1)����A.
(2)������x2+y2=1�ھ��A��׃�Q�µõ�������������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ �У�ֱ��
�У�ֱ�� �ھ��
�ھ�� ��(du��)��(y��ng)��׃�Q�����µõ�ֱ��
��(du��)��(y��ng)��׃�Q�����µõ�ֱ��
 ����(sh��)��(sh��)
����(sh��)��(sh��) ��
�� ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��������(sh��) ��
�� �������ų�
�������ų�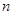 ��
��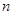 �еĔ�(sh��)��.��(du��)��ijһ��(g��)��(sh��)����Ӌ(j��)����к����е�����ɂ�(g��)��(sh��)
�еĔ�(sh��)��.��(du��)��ijһ��(g��)��(sh��)����Ӌ(j��)����к����е�����ɂ�(g��)��(sh��) ��
�� ���ı�ֵ
���ı�ֵ ���Q(ch��ng)�@Щ��ֵ�е���Сֵ���@��(g��)��(sh��)���ġ�����ֵ��.��
���Q(ch��ng)�@Щ��ֵ�е���Сֵ���@��(g��)��(sh��)���ġ�����ֵ��.�� ��ʾij��(g��)
��ʾij��(g��)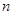 ��
��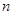 �Д�(sh��)���е�
�Д�(sh��)���е� �е�
�е� �еĔ�(sh��)��
�еĔ�(sh��)�� ��
�� �����ҝM(m��n)��
�����ҝM(m��n)�� ����(d��ng)
����(d��ng) �r(sh��)��(sh��)���ġ�����ֵ����_(k��i)________
�r(sh��)��(sh��)���ġ�����ֵ����_(k��i)________
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)���M�� (����a>0��b>0)��
(����a>0��b>0)��
(1)��a��2��b��3������M������M��1��
(2)������C��x2��y2��1�ھ��M����(du��)��(y��ng)�ľ���׃�Q�����µõ�����C�䣺 ��y2��1����a��b��ֵ��
��y2��1����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��ֱ֪�� �ھ��
�ھ�� ��(du��)��(y��ng)��׃�Q������׃?y��u)�ֱ��
��(du��)��(y��ng)��׃�Q������׃?y��u)�ֱ��
��I����(sh��)��(sh��) ��ֵ
��ֵ
��II�����c(di��n) ��ֱ��
��ֱ�� �ϣ���
�ϣ��� �����c(di��n)
�����c(di��n) ������(bi��o)
������(bi��o)
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com