
已知常數(shù) 、
、 、
、 都是實數(shù),函數(shù)
都是實數(shù),函數(shù) 的導函數(shù)為
的導函數(shù)為 ,
, 的解集為
的解集為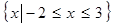 .
.
(Ⅰ)若 的極大值等于
的極大值等于 ,求
,求 的極小值;
的極小值;
(Ⅱ)設不等式 的解集為集合
的解集為集合 ,當
,當 時,函數(shù)
時,函數(shù) 只有一個零點,求實數(shù)
只有一個零點,求實數(shù) 的取值范圍.
的取值范圍.
(Ⅰ)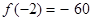 ;(Ⅱ)當
;(Ⅱ)當 或
或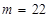 時,函數(shù)
時,函數(shù)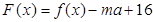 在
在 上只有一個零點.
上只有一個零點.
【解析】
試題分析::1.第(Ⅰ)的解答還是要破費周折的.首先要求出導函數(shù)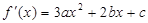 .
.
然后根據(jù)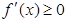 的解集為
的解集為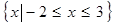 ,通過解混合組,得到
,通過解混合組,得到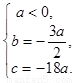 進而得到
進而得到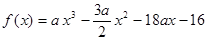 .接下來通過研究函數(shù)
.接下來通過研究函數(shù)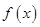 的單調性,由
的單調性,由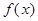 的極大值等于
的極大值等于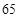 ,可解得
,可解得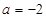 ,這樣就可以求出
,這樣就可以求出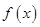 的極小值
的極小值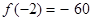 .2.第(Ⅱ)問先由不等式
.2.第(Ⅱ)問先由不等式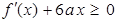 的解集為集合
的解集為集合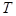 ,可以解得
,可以解得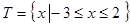 .然后研究
.然后研究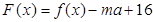 的單調性,值得注意的是
的單調性,值得注意的是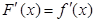 ,換句話說方程兩邊對
,換句話說方程兩邊對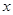 求導數(shù),
求導數(shù), 、
、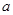 應看作是常數(shù).單調性弄清楚后,還要比較
應看作是常數(shù).單調性弄清楚后,還要比較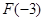 、
、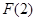 的大小.然后根據(jù)
的大小.然后根據(jù)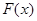 只有一個零點,列出
只有一個零點,列出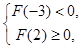 或
或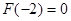 ,最后解之即可.值得注意的是,很多考生漏了
,最后解之即可.值得注意的是,很多考生漏了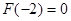 .
.
試題解析:(Ⅰ)∵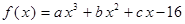 ,∴
,∴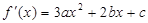 .
.
∵不等式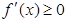 的解集為
的解集為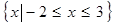 ,
,
∴不等式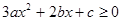 的解集為
的解集為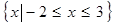 .
.
∴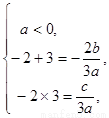 即
即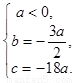
∴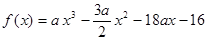 ,
,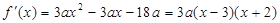 .
.
∴當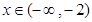 或
或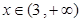 時,
時,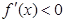 ,即
,即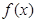 為單調遞減函數(shù);
為單調遞減函數(shù);
當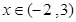 時,
時, ,即
,即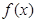 為單調遞增函數(shù).
為單調遞增函數(shù).
∴當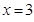 時,
時,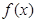 取得極大值,當
取得極大值,當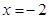 時,
時,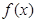 取得極小值.
取得極小值.
由已知得 ,解得
,解得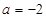 .
.
∴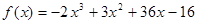 .
.
∴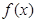 的極小值
的極小值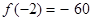 .
.
(Ⅱ)∵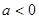 ,
, ,
,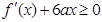 ,
,
∴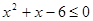 ,解得
,解得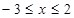 ,即
,即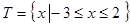 .
.
∵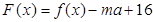 ,∴
,∴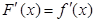 .
.
∴當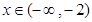 或
或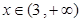 時,
時,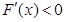 ,即
,即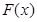 為單調遞減函數(shù);
為單調遞減函數(shù);
當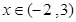 時,
時, ,即
,即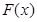 為單調遞增函數(shù).
為單調遞增函數(shù).
∴當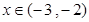 時,
時,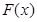 為單調遞減函數(shù);
為單調遞減函數(shù);
當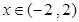 時,
時,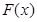 為單調遞增函數(shù).
為單調遞增函數(shù).
∵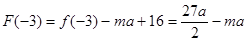 ,
,
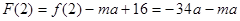 ,
,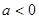 ,
,
∴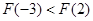 .
.
∴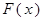 在
在 上只有一個零點
上只有一個零點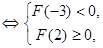 或
或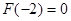 .
.
由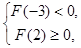 得
得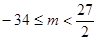 ;
;
由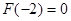 ,即
,即 ,得
,得 .
.
∴實數(shù) 的取值范圍為
的取值范圍為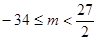 或
或 .
.
∴當 或
或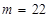 時,函數(shù)
時,函數(shù)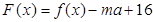 在
在 上只有一個零點.
上只有一個零點.
考點:本題通過導數(shù)綜合考查函數(shù)的單調性、極值、零點、比較大小等知識.


科目:高中數(shù)學 來源: 題型:
已知常數(shù)![]() 、
、![]() 、
、![]() 都是實數(shù),函數(shù)
都是實數(shù),函數(shù)![]() 的導函數(shù)為
的導函數(shù)為![]()
(Ⅰ)設![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(Ⅱ)如果方程![]() 的兩個實數(shù)根分別為
的兩個實數(shù)根分別為![]() 、
、![]() ,并且
,并且![]()
問:是否存在正整數(shù)![]() ,使得
,使得![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源:2012-2013學年云南省畢業(yè)生復習第二次統(tǒng)一檢測理科數(shù)學試卷(解析版) 題型:選擇題
已知常數(shù) 、
、 、
、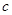 都是實數(shù),
都是實數(shù), 的導函數(shù)為
的導函數(shù)為 ,
, 的解集為
的解集為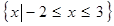 ,若
,若 的極小值等于
的極小值等于 ,則
,則 的值是( )
的值是( )
(A) (B)
(B)
(C) (D)
(D)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
已知常數(shù)![]() 、
、![]() 、
、![]() 都是實數(shù),函數(shù)
都是實數(shù),函數(shù)![]() 的導函數(shù)為
的導函數(shù)為![]()
(Ⅰ)設![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(Ⅱ)如果方程![]() 的兩個實數(shù)根分別為
的兩個實數(shù)根分別為![]() 、
、![]() ,并且
,并且![]()
問:是否存在正整數(shù)![]() ,使得
,使得![]() ?請說明理由.
?請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(14分)已知常數(shù)![]() 、
、![]() 、
、![]() 都是實數(shù),函數(shù)
都是實數(shù),函數(shù)![]() 的導函數(shù)為
的導函數(shù)為![]()
(Ⅰ)設![]() ,求函數(shù)f(x)的解析式;
,求函數(shù)f(x)的解析式;
(Ⅱ)設 ![]() ,且
,且![]() ,求
,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com