
(05年遼寧卷)(14分)
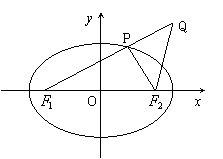
已知橢圓![]() 的左、右焦點(diǎn)分別是
的左、右焦點(diǎn)分別是
![]() 、
、![]() ,
,![]() 是橢圓外的動點(diǎn),滿足
是橢圓外的動點(diǎn),滿足![]() ,
,
點(diǎn)P是線段![]() 與該橢圓的交點(diǎn),點(diǎn)T在線段
與該橢圓的交點(diǎn),點(diǎn)T在線段![]() 上,并且
上,并且
滿足![]() .
.
(Ⅰ)設(shè)![]() 為點(diǎn)P的橫坐標(biāo),證明
為點(diǎn)P的橫坐標(biāo),證明 ![]() ;
;
(Ⅱ)求點(diǎn)T的軌跡C的方程;
(Ⅲ)試問:在點(diǎn)T的軌跡C上,是否存在點(diǎn)M,使△![]() 的面積
的面積![]() .若存在,求
.若存在,求
∠![]() 的正切值;若不存在,請說明理由.
的正切值;若不存在,請說明理由.

解析:(Ⅰ)證法一:設(shè)點(diǎn)P的坐標(biāo)為![]()
由P![]() 在橢圓上,得
在橢圓上,得
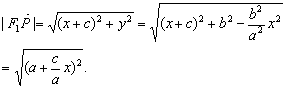
由![]() ,所以
,所以 ![]() ……3分
……3分
證法二:設(shè)點(diǎn)P的坐標(biāo)為![]() 記
記![]()
則![]()
由![]() ,得
,得
![]() .
.
證法三:設(shè)點(diǎn)P的坐標(biāo)為![]()
橢圓的左準(zhǔn)線方程為![]()
由橢圓第二定義得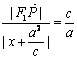 ,即
,即![]()
由![]() ,所以
,所以![]() ……3分
……3分
(Ⅱ)解法一:設(shè)點(diǎn)T的坐標(biāo)為![]()
當(dāng)![]() 時(shí),點(diǎn)(
時(shí),點(diǎn)(![]() ,0)和點(diǎn)(-
,0)和點(diǎn)(-![]() ,0)在軌跡上.
,0)在軌跡上.
當(dāng)|![]() 時(shí),
時(shí),
由![]() ,得
,得![]() .
.
又![]() ,所以T為線段F2Q的中點(diǎn).
,所以T為線段F2Q的中點(diǎn).
在△QF1F2中,![]() ,所以有
,所以有![]()
綜上所述,點(diǎn)T的軌跡C的方程是![]() ……7分
……7分
解法二:設(shè)點(diǎn)T的坐標(biāo)為![]() 當(dāng)
當(dāng)![]() 時(shí),點(diǎn)(
時(shí),點(diǎn)(![]() ,0)和點(diǎn)(-
,0)和點(diǎn)(-![]() ,0)在軌跡上.
,0)在軌跡上.
當(dāng)|![]() 時(shí),由
時(shí),由![]() ,得
,得![]() .
.
又![]() ,所以T為線段F2Q的中點(diǎn).
,所以T為線段F2Q的中點(diǎn).
設(shè)點(diǎn)Q的坐標(biāo)為(![]() ),則
),則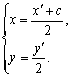
因此![]() ①
①
由![]() 得
得![]() ②
②
將①代入②,可得![]()
綜上所述,點(diǎn)T的軌跡C的方程是![]() ……7分
……7分
|
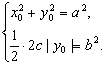
由③得![]() ,
,
由④得![]()
所以,當(dāng)![]() 時(shí),存在點(diǎn)M,使S=
時(shí),存在點(diǎn)M,使S=![]() ;
;
當(dāng)![]() 時(shí),不存在滿足條件的點(diǎn)M. ……11分
時(shí),不存在滿足條件的點(diǎn)M. ……11分
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
由![]() ,
,
![]() ,
,
![]() ,得
,得
![]()
解法二:
C上存在點(diǎn)M(![]() )使S=
)使S=![]() 的充要條件是
的充要條件是
|
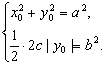
由④得![]() 上式代入③得
上式代入③得
![]()
于是,當(dāng)![]() 時(shí),存在點(diǎn)M,使S=
時(shí),存在點(diǎn)M,使S=![]() ;
;
當(dāng)![]() 時(shí),不存在滿足條件的點(diǎn)M. ……11分
時(shí),不存在滿足條件的點(diǎn)M. ……11分
當(dāng)![]() 時(shí),記
時(shí),記![]() ,
,
由![]() 知
知![]() ,所以
,所以
![]() ……14分
……14分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
(09年江蘇百校樣本分析)(10分)挑選空軍飛行學(xué)員可以說是“萬里挑一”,要想通過需過“五關(guān)”――目測、初檢、復(fù)檢、文考、政審等. 某校甲、乙、丙三個(gè)同學(xué)都順利通過了前兩關(guān),有望成為光榮的空軍飛行學(xué)員. 根據(jù)分析,甲、乙、丙三個(gè)同學(xué)能通過復(fù)檢關(guān)的概率分別是0.5,0.6,0.75,能通過文考關(guān)的概率分別是0.6,0.5,0.4,通過政審關(guān)的概率均為1.后三關(guān)相互獨(dú)立.
(1)求甲、乙、丙三個(gè)同學(xué)中恰有一人通過復(fù)檢的概率;
(2)設(shè)通過最后三關(guān)后,能被錄取的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的期望
的期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年江蘇百校樣本分析)(10分)(矩陣與變換) 給定矩陣 A=![]() ,
,![]() =
=![]() .
.
(1)求A的特征值![]() 、
、![]() 及對應(yīng)的特征向量
及對應(yīng)的特征向量![]() ;
;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(08年莆田四中一模理) (14分)
由函數(shù)![]() 確定數(shù)列
確定數(shù)列![]() ,
,![]() ,若函數(shù)
,若函數(shù)![]() 的反函數(shù)
的反函數(shù)![]() 能確定數(shù)列
能確定數(shù)列![]() ,
,![]() ,則稱數(shù)列
,則稱數(shù)列![]() 是數(shù)列
是數(shù)列![]() 的“反數(shù)列”。
的“反數(shù)列”。
(1)若函數(shù)![]() 確定數(shù)列
確定數(shù)列![]() 的反數(shù)列為
的反數(shù)列為![]() ,求
,求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)對(1)中![]() ,不等式
,不等式![]() 對任意的正整數(shù)
對任意的正整數(shù)![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的范圍;
的范圍;
(3)設(shè)![]() ,若數(shù)列
,若數(shù)列![]() 的反數(shù)列為
的反數(shù)列為![]() ,
,![]() 與
與![]() 的公共項(xiàng)組成的數(shù)列為
的公共項(xiàng)組成的數(shù)列為![]() ;求數(shù)列
;求數(shù)列![]() 前
前![]() 項(xiàng)和
項(xiàng)和![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(05年遼寧卷)(12分)
已知函數(shù)![]() .設(shè)數(shù)列
.設(shè)數(shù)列![]() 滿足
滿足![]() ,
,![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足
![]() ,
,![]() …
…![]() ,
,
(Ⅰ)用數(shù)學(xué)歸納法證明![]() ;(Ⅱ)證明
;(Ⅱ)證明 ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(05年湖北卷文)(12分)
設(shè)數(shù)列![]() 的前n項(xiàng)和為Sn=2n2,
的前n項(xiàng)和為Sn=2n2,![]() 為等比數(shù)列,且
為等比數(shù)列,且![]()
(Ⅰ)求數(shù)列![]() 和
和![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè)![]() ,求數(shù)列
,求數(shù)列![]() 的前n項(xiàng)和Tn.
的前n項(xiàng)和Tn.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com