
(1)求x0關(guān)于t的函數(shù)x0=f(x)的表達(dá)式,判斷函數(shù)f(t)的單調(diào)性,并證明你的判斷;
(2)設(shè)△OFG的面積S=![]() t,若以O(shè)為中心,F(xiàn)為焦點(diǎn)的橢圓經(jīng)過點(diǎn)G,求當(dāng)|
t,若以O(shè)為中心,F(xiàn)為焦點(diǎn)的橢圓經(jīng)過點(diǎn)G,求當(dāng)|![]() |取得最小值時(shí)橢圓的方程;
|取得最小值時(shí)橢圓的方程;
(3)在(2)的條件下,若點(diǎn)P的坐標(biāo)為(0,92),C、D是橢圓上的兩點(diǎn),且![]() =λ
=λ![]() (λ≠1),求實(shí)數(shù)λ的取值范圍.
(λ≠1),求實(shí)數(shù)λ的取值范圍.
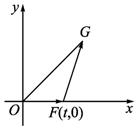
解:(1)由題意,![]() =(x0-t,y0),
=(x0-t,y0),![]() =(t,0),
=(t,0),
則![]() ·
·![]() =t(x0-t)=1,∴x0=f(t)=t+
=t(x0-t)=1,∴x0=f(t)=t+![]() .
.
設(shè)3≤t1<t2,則f(t2)-f(t1)=(t2+![]() )-(t1+
)-(t1+![]() )=
)=![]() .
.
∵t2-t1>0,t1t2-1>0,t1t2>0,∴f(t2)-f(t1)>0,f(t2)>f(t1),
∴f(t)在[3,+∞)上單調(diào)遞增.
(2)由S=![]() |
|![]() ||y0|=
||y0|=![]() t·|y0|=
t·|y0|=![]() t,得y0=±
t,得y0=±![]() ,
,
∴點(diǎn)G的坐標(biāo)為(t+![]() ,±
,±![]() ),|
),|![]() |2=(t+
|2=(t+![]() )2+
)2+![]() .
.
∵f(t)在[3,+∞]上單調(diào)遞增,
∴當(dāng)t=3時(shí),|![]() |取得最小值,此時(shí)F、G的坐標(biāo)分別是(3,0)、(
|取得最小值,此時(shí)F、G的坐標(biāo)分別是(3,0)、(![]() ,±
,±![]() ).
).
由題意設(shè)橢圓方程為![]() =1,由點(diǎn)G在橢圓上得
=1,由點(diǎn)G在橢圓上得![]() =1,解得b2=9,
=1,解得b2=9,
∴所求橢圓方程為![]() =1.
=1.
(3)方法1:設(shè)C、D的坐標(biāo)分別為(x,y)、(m,n),則![]() =(x,y-
=(x,y-![]() ),
),![]() =(m,n-
=(m,n-![]() ).
).
由![]() =λ
=λ![]() ,得(x,y-
,得(x,y-![]() )=λ(m,n-
)=λ(m,n-![]() ),x=λm,y=λn-
),x=λm,y=λn-![]() λ+
λ+![]() .
.
∵C、D在橢圓上,∴![]() =1,
=1,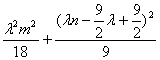 =1,消去m得 n=
=1,消去m得 n=![]() .
.
又∵|n|≤3,∴|![]() |≤3,解得
|≤3,解得![]() ≤λ≤5,∴實(shí)數(shù)λ的取值范圍是[
≤λ≤5,∴實(shí)數(shù)λ的取值范圍是[![]() ,1)∪(1,5].
,1)∪(1,5].
方法2:記點(diǎn)A、B的坐標(biāo)分別為(0,3)、(0,-3),過點(diǎn)A、B分別作y軸的垂線,交直線PC于點(diǎn)M、N.
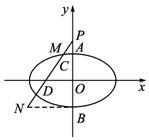
若|![]() |<|
|<|![]() |,則|
|,則|![]() |≤|
|≤|![]() |,|
|,|![]() |≥|
|≥|![]() |,
|,
∴1<![]() ≤
≤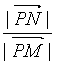 =
=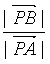 =5,則1<
=5,則1<![]() ≤5,
≤5,![]() ≤λ<1;
≤λ<1;
若|![]() |>|
|>|![]() |,同理可得1<
|,同理可得1<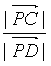 ≤
≤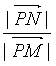 =
=![]() =5,則1<λ≤5.
=5,則1<λ≤5.
綜上,實(shí)數(shù)λ的取值范圍是[![]() ,1)∪(1,5].
,1)∪(1,5].


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
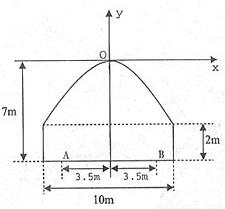
 如圖所示,一隧道內(nèi)設(shè)雙行線公路,其截面由長方形的三條邊和拋物線的一段構(gòu)成,為保證安全,要求行駛車輛頂部(設(shè)為平頂)與隧道頂部在豎直方向上高度之差至少要有0.5米.
如圖所示,一隧道內(nèi)設(shè)雙行線公路,其截面由長方形的三條邊和拋物線的一段構(gòu)成,為保證安全,要求行駛車輛頂部(設(shè)為平頂)與隧道頂部在豎直方向上高度之差至少要有0.5米.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2008-2009學(xué)年福建省泉州市惠安縣惠南中學(xué)高二(上)期末數(shù)學(xué)試卷(選修2-1)(理科)(解析版) 題型:解答題
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com