
函數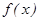 的定義域為D,若存在閉區間[a,b]
的定義域為D,若存在閉區間[a,b]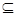 D,使得函數
D,使得函數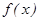 滿足:(1)
滿足:(1)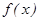 在[a,b]內是單調函數;(2)
在[a,b]內是單調函數;(2)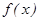 在[a,b]上的值域為[2a,2b],則稱區間[a,b]為y=
在[a,b]上的值域為[2a,2b],則稱區間[a,b]為y=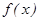 的“美麗區間”.下列函數中存在“美麗區間”的是 . (只需填符合題意的函數序號)
的“美麗區間”.下列函數中存在“美麗區間”的是 . (只需填符合題意的函數序號)
①、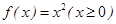 ; ②、
; ②、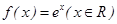 ;
;
③、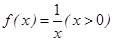 ; ④、
; ④、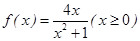 .
.
①③④
解析試題分析:函數中存在“美麗區間”的定義可知:①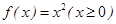 在[a,b]內是單調增函數;
在[a,b]內是單調增函數;
則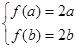 ,解得
,解得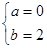 ∴f(x)=x2(x≥0),若存在“美麗區間”[0,2],∴f(x)=x2(x≥0),若存在“美麗區間”[0,2];②f(x)=ex(x∈R),若存在“美麗區間”[a,b],則
∴f(x)=x2(x≥0),若存在“美麗區間”[0,2],∴f(x)=x2(x≥0),若存在“美麗區間”[0,2];②f(x)=ex(x∈R),若存在“美麗區間”[a,b],則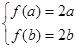 ,所以
,所以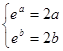 ,構建函數g(x)=ex-2x,∴g′(x)=ex-2,∴函數在(-∞,ln2)上單調減,在(ln2,+∞)上單調增,∴函數在x=ln2處取得極小值,且為最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0無解,故函數不存在“美麗區間”;③
,構建函數g(x)=ex-2x,∴g′(x)=ex-2,∴函數在(-∞,ln2)上單調減,在(ln2,+∞)上單調增,∴函數在x=ln2處取得極小值,且為最小值.∵g(ln2)=2-2ln2>0,∴g(x)>0恒成立,∴ex-2x=0無解,故函數不存在“美麗區間”;③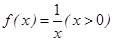 在
在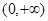 上單調遞減,若存在“美麗區間”[a,b],則
上單調遞減,若存在“美麗區間”[a,b],則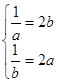 ,則
,則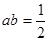 ,故存在;④
,故存在;④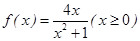 ,
,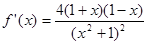 ,若存在“倍值區間”[a,b]⊆[0,1],則
,若存在“倍值區間”[a,b]⊆[0,1],則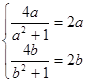 ∴a=0,b=1,若存在“美麗區間”[0,1];故存在“美麗區間”的是①③④.
∴a=0,b=1,若存在“美麗區間”[0,1];故存在“美麗區間”的是①③④.
考點:1.函數的值域 ;2.函數的單調性


科目:高中數學 來源: 題型:填空題
有下列四個命題:
①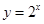 與
與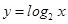 互為反函數,其圖象關于直線
互為反函數,其圖象關于直線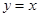 對稱;
對稱;
②已知函數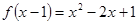 ,則
,則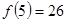 ;
;
③當 且
且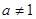 時,函數
時,函數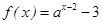 必過定點(2,-2);
必過定點(2,-2);
④函數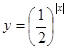 的值域是(0,+
的值域是(0,+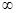 );
);
你認為正確命題的序號是 (把正確的序號都寫上)
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
對于具有相同定義域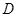 的函數
的函數 和
和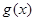 ,若存在
,若存在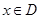 ,使得
,使得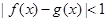 ,則
,則 和
和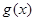 在
在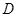 上是“親密函數”.給出定義域均為
上是“親密函數”.給出定義域均為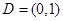 的四組函數如下:
的四組函數如下:
①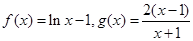 ②
②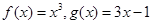
③ 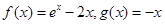 ④
④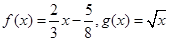
其中,函數 和
和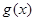 在
在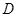 上是“親密函數”的是 .
上是“親密函數”的是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com