
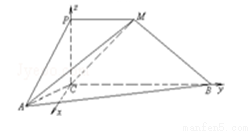
如圖,四邊形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2.又AC=1,∠ACB=120°,AB⊥PC,直線AM與直線PC所成的角為60°.
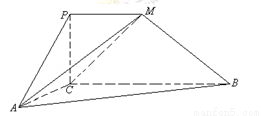
(1)求證:PC⊥AC;
(2)求二面角M﹣AC﹣B的余弦值;
(3)求點B到平面MAC的距離.
(1)詳見解析;(2)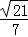 ;(3)
;(3)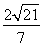
【解析】
試題分析:(1)先根據線面垂直的判定定理證PC⊥平面ABC,即可證得PC⊥AC。(2)用空間向量法求二面角。先過C作BC的垂線,建立空間直角坐標系,再求各點的坐標,和各向量的坐標,再根據向量垂直的數量積公式求面的法向量,但需注意兩法向量所成的角和二面角相等或互補。(3)在(2)中已求出面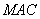 的一個法向量
的一個法向量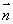 ,根據
,根據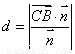 可求其距離。
可求其距離。
試題解析:【解析】
(1)證明:∵PC⊥BC,PC⊥AB, ∴PC⊥平面ABC,∵
∴PC⊥平面ABC,∵ ∴PC⊥AC. 2分
∴PC⊥AC. 2分
(2)在平面ABC內,過C作BC的垂線,并建立空間直角坐標系如圖所示.
設P(0,0,z),則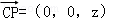 .
.
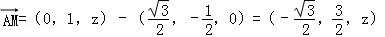 .
.
∵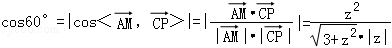 ,
,
且z>0,∴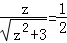 ,得z=1,∴
,得z=1,∴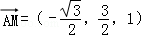 .
.
設平面MAC的一個法向量為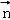 =(x,y,1),則由
=(x,y,1),則由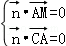
得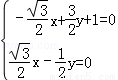 得
得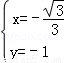 ∴
∴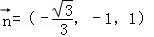 .
.
平面ABC的一個法向量為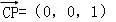 .
.
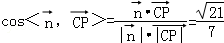 .
.
顯然,二面角M﹣AC﹣B為銳二面角,∴二面角M﹣AC﹣B的余弦值為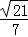 . 8分
. 8分
(3)點B到平面MAC的距離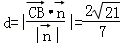 . 12分
. 12分
考點:1線線垂直、線面垂直;2空間向量法解決立體幾何問題。


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十二第十章第九節練習卷(解析版) 題型:選擇題
若隨機變量X~B(100,p),X的數學期望E(X)=24,則p的值是( )
(A) (B)
(B) (C)
(C)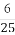 (D)
(D)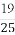
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業七十一第十章第八節練習卷(解析版) 題型:選擇題
一只袋內裝有m個白球,n-m個黑球,連續不放回地從袋中取球,直到取出黑球為止,設此時取出了ξ個白球,下列概率等于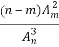 的是( )
的是( )
(A)P(ξ=3) (B)P(ξ≥2)
(C)P(ξ≤3) (D)P(ξ=2)
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知函數
(1)若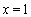 為
為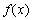 的極值點,求
的極值點,求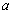 的值;
的值;
(2)若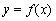 的圖象在點
的圖象在點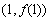 處的切線方程為
處的切線方程為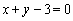 ,
,
①求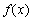 在區間
在區間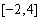 上的最大值;
上的最大值;
②求函數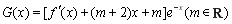 的單調區間.
的單調區間.
查看答案和解析>>
科目:高中數學 來源:2014年高中數學全國各省市理科導數精選22道大題練習卷(解析版) 題型:解答題
已知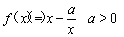 ,
,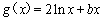 ,且直線
,且直線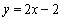 與曲線
與曲線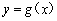 相切.
相切.
(1)若對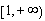 內的一切實數
內的一切實數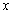 ,不等式
,不等式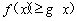 恒成立,求實數
恒成立,求實數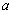 的取值范圍;
的取值范圍;
(2)當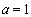 時,求最大的正整數
時,求最大的正整數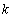 ,使得對
,使得對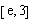 (
(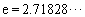 是自然對數的底數)內的任意
是自然對數的底數)內的任意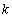 個實數
個實數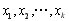 都有
都有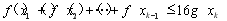 成立;
成立;
(3)求證: .
.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:填空題
已知函數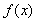 =x+sinx.項數為19的等差數列
=x+sinx.項數為19的等差數列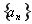 滿足
滿足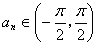 ,且公差
,且公差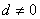 .若
.若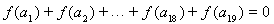 ,則當
,則當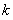 =__________時,
=__________時,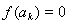 .
.
查看答案和解析>>
科目:高中數學 來源:2014年陜西省咸陽市高考模擬考試(一)理科數學試卷(解析版) 題型:選擇題
已知A={x|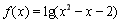 ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|<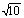 ,i為虛數單位,x>0},則A
,i為虛數單位,x>0},則A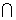 B=( )
B=( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中數學 來源:2013-2014學年(安徽專用)高考數學(文)仿真模擬卷2練習卷(解析版) 題型:填空題
一次射擊訓練,某小組的成績只有7環、8環、9環三種情況,且該小組的平均成績為8.15環,設該小組成績為7環的有x人,成績為8環、9環的人數情況見下表:
環數(環) | 8 | 9 |
人數(人) | 7 | 8 |
那么x=________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com