
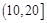 ,2;
,2;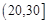 ,3;
,3; ,4;
,4; ,5;
,5; ,4;
,4;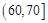 ,2.則樣本在
,2.則樣本在 上的頻率是 .
上的頻率是 . 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源:不詳 題型:解答題
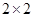 列聯表;
列聯表;查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
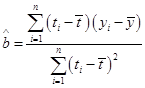 ,
,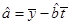
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 元/張
元/張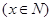 ,則“足球迷”中非“鐵桿足球迷”愿意前往觀看的人數會減少
,則“足球迷”中非“鐵桿足球迷”愿意前往觀看的人數會減少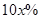 ,“鐵桿足球迷”愿意前往觀看的人數會減少
,“鐵桿足球迷”愿意前往觀看的人數會減少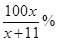 .問票價至少定為多少元/張時,才能使前往現場觀看足球比賽的人數不超過10萬人?
.問票價至少定為多少元/張時,才能使前往現場觀看足球比賽的人數不超過10萬人?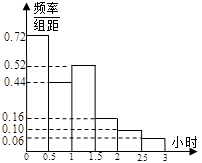
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
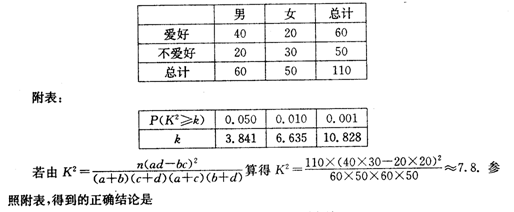
| A.有99%以上的把握認為“愛好該項運動與性別有關” |
| B.有99%以上的把握認為“愛好該項運動與性別無關” |
| C.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關” |
| D.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關” |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
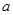 表示.
表示.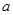 的值;
的值;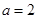 時,分別從甲,乙兩組同學中各隨機選取一名同學,求這兩名同學的數學成績之差的絕對值不超過2分的概率.
時,分別從甲,乙兩組同學中各隨機選取一名同學,求這兩名同學的數學成績之差的絕對值不超過2分的概率.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題

| 零件數x(個) | 10 | 20 | 30 | 40 | 50 |
| 加工時間y(min) | 62 | m | n | 81 | 89 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
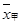 、
、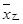 表示,則下列結論正確的是( )
表示,則下列結論正確的是( )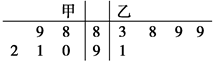
A.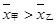 ,且甲比乙成績穩定 ,且甲比乙成績穩定 | B.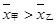 ,且乙比甲成績穩定 ,且乙比甲成績穩定 |
C.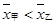 ,且甲比乙成績穩定 ,且甲比乙成績穩定 | D.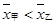 ,且乙比甲成績穩定 ,且乙比甲成績穩定 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 年齡/周歲 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 身高/cm | 91.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
| | |||||||
| 年齡/周歲 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com