
為了尋找馬航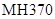 殘骸,我國“雪龍?zhí)枴笨瓶即?014年3月26日從港口
殘骸,我國“雪龍?zhí)枴笨瓶即?014年3月26日從港口 出發(fā),沿北偏東
出發(fā),沿北偏東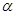 角的射線
角的射線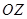 方向航行,而在港口北偏東
方向航行,而在港口北偏東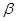 角的方向上有一個給科考船補(bǔ)給物資的小島
角的方向上有一個給科考船補(bǔ)給物資的小島 ,
,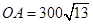 海里,且
海里,且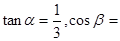
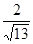 .現(xiàn)指揮部需要緊急征調(diào)位于港口
.現(xiàn)指揮部需要緊急征調(diào)位于港口 正東
正東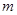 海里的
海里的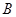 處的補(bǔ)給船,速往小島
處的補(bǔ)給船,速往小島 裝上補(bǔ)給物資供給科考船.該船沿
裝上補(bǔ)給物資供給科考船.該船沿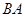 方向全速追趕科考船,并在
方向全速追趕科考船,并在 處相遇.經(jīng)測算當(dāng)兩船運行的航線與海岸線
處相遇.經(jīng)測算當(dāng)兩船運行的航線與海岸線 圍成的三角形
圍成的三角形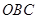 的面積
的面積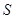 最小時,這種補(bǔ)給方案最優(yōu).
最小時,這種補(bǔ)給方案最優(yōu).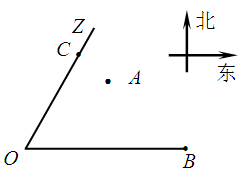
(1)求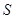 關(guān)于
關(guān)于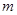 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式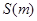 ;
;
(2)應(yīng)征調(diào)位于港口正東多少海里處的補(bǔ)給船只,補(bǔ)給方案最優(yōu)?
(1)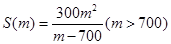 ;(2)1400.
;(2)1400.
解析試題分析:(1)本題已知條件可以理解為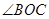 是固定的,點
是固定的,點 也是不變,直線
也是不變,直線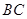 過點
過點 ,要求
,要求 面積的最小值,根據(jù)已知條件,我們用解析法來解題,以
面積的最小值,根據(jù)已知條件,我們用解析法來解題,以 為坐標(biāo)原點,向東方向為
為坐標(biāo)原點,向東方向為 正半軸,向北方向為
正半軸,向北方向為 軸正半軸,建立直角坐標(biāo)系,則可得直線
軸正半軸,建立直角坐標(biāo)系,則可得直線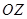 的方程為
的方程為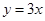 ,點
,點 坐標(biāo)為
坐標(biāo)為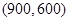 ,又有點
,又有點 坐標(biāo)為
坐標(biāo)為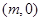 ,可得直線
,可得直線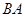 方程,它與直線
方程,它與直線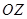 的交點
的交點 的坐標(biāo)可解得,而
的坐標(biāo)可解得,而 ,這樣要求的表達(dá)式就可得;(2)在(1)基礎(chǔ)上,
,這樣要求的表達(dá)式就可得;(2)在(1)基礎(chǔ)上,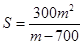 ,其最小值求法,把分式的分子分母同時除以
,其最小值求法,把分式的分子分母同時除以 ,得
,得 ,分母是關(guān)于
,分母是關(guān)于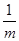 的二次函數(shù),最值易求.
的二次函數(shù),最值易求.
試題解析:(1)以O(shè)點為原點,正北的方向為y軸正方向建立直角坐標(biāo)系, (1分)
則直線OZ的方程為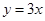 ,設(shè)點A(x0,y0),則
,設(shè)點A(x0,y0),則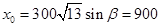 ,
,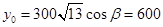 ,即A(900,600), (3分)
,即A(900,600), (3分)
又B(m,0),則直線AB的方程為: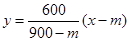 , (4分)
, (4分)
由此得到C點坐標(biāo)為: , (6分)
, (6分)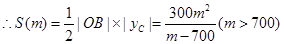 (8分)
(8分)
(2)由(1)知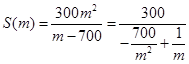 (10分)
(10分)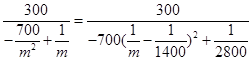 (12分)
(12分)
所以當(dāng)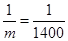 ,即
,即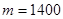 時,
時,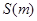 最小,
最小,
(或令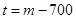 ,則
,則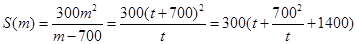
 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)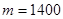 時,
時,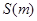 最小)
最小)
∴征調(diào)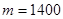 海里處的船只時,補(bǔ)給方案最優(yōu). (14分)
海里處的船只時,補(bǔ)給方案最優(yōu). (14分)
考點:解析法解應(yīng)用題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
經(jīng)過長期觀測得到:在交通繁忙的時段內(nèi),某公路段汽車的車流量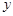 (千輛/時)與汽車的平均速度
(千輛/時)與汽車的平均速度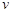 (千米/時)之間的函數(shù)關(guān)系為
(千米/時)之間的函數(shù)關(guān)系為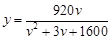 (
(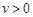 ).
).
(1)在該時段內(nèi),當(dāng)汽車的平均速度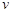 為多少時,車流量最大?最大車流量為多少?
為多少時,車流量最大?最大車流量為多少?
(2)若要求在該時段內(nèi)車流量超過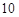 千輛/時,則汽車的平均速度應(yīng)在什么范圍內(nèi)?
千輛/時,則汽車的平均速度應(yīng)在什么范圍內(nèi)?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知中心在原點,焦點在 軸上的橢圓
軸上的橢圓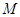 的離心率為
的離心率為 ,橢圓上異于長軸頂點的任意點
,橢圓上異于長軸頂點的任意點 與左右兩焦點
與左右兩焦點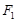 、
、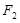 構(gòu)成的三角形中面積的最大值為
構(gòu)成的三角形中面積的最大值為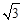 .
.
(1)求橢圓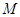 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知點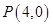 ,連接
,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,若
,若 與橢圓相切時
與橢圓相切時 、
、 不重合,連接
不重合,連接 與橢圓的另一交點記為
與橢圓的另一交點記為 ,求
,求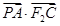 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(2011•湖北)提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數(shù),當(dāng)橋上的車流密度達(dá)到200輛/千米時,造成堵塞,此時車流速度為0;當(dāng)車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當(dāng)20≤x≤200時,車流速度v是車流密度x的一次函數(shù).
(1)當(dāng)0≤x≤200時,求函數(shù)v(x)的表達(dá)式;
(2)當(dāng)車流密度x為多大時,車流量(單位時間內(nèi)通過橋上某觀測點的車輛數(shù),單位:輛/小時)f(x)=x•v(x)可以達(dá)到最大,并求出最大值.(精確到1輛/小時).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù)f(x)=ax2+bx+c (a≠0)且滿足f(-1)=0,對任意實數(shù)x,恒有f(x)-x≥0,并且當(dāng)x∈(0,2)時,f(x)≤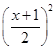 .
.
(1)求f(1)的值;
(2)證明:a>0,c>0;
(3)當(dāng)x∈[-1,1]時,函數(shù)g(x)=f(x)-mx (x∈R)是單調(diào)函數(shù),求證:m≤0或m≥1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,某小區(qū)有一邊長為2(單位:百米)的正方形地塊OABC,其中OAE是一個游泳池,計劃在地塊OABC內(nèi)修一條與池邊AE相切的直路 (寬度不計),切點為M,并把該地塊分為兩部分.現(xiàn)以點O為坐標(biāo)原點,以線段OC所在直線為x軸,建立平面直角坐標(biāo)系,若池邊AE滿足函數(shù)
(寬度不計),切點為M,并把該地塊分為兩部分.現(xiàn)以點O為坐標(biāo)原點,以線段OC所在直線為x軸,建立平面直角坐標(biāo)系,若池邊AE滿足函數(shù) )的圖象,且點M到邊OA距離為
)的圖象,且點M到邊OA距離為 .
.
(1)當(dāng) 時,求直路
時,求直路 所在的直線方程;
所在的直線方程;
(2)當(dāng)t為何值時,地塊OABC在直路 不含泳池那側(cè)的面積取到最大,最大值是多少?
不含泳池那側(cè)的面積取到最大,最大值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某市2013年發(fā)放汽車牌照12萬張,其中燃油型汽車牌照10萬張,電動型汽車2萬張.為了節(jié)能減排和控制總量,從2013年開始,每年電動型汽車牌照按50%增長,而燃油型汽車牌照每一年比上一年減少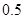 萬張,同時規(guī)定一旦某年發(fā)放的牌照超過15萬張,以后每一年發(fā)放的電動車的牌照的數(shù)量維持在這一年的水平不變.
萬張,同時規(guī)定一旦某年發(fā)放的牌照超過15萬張,以后每一年發(fā)放的電動車的牌照的數(shù)量維持在這一年的水平不變.
(1)記2013年為第一年,每年發(fā)放的燃油型汽車牌照數(shù)構(gòu)成數(shù)列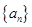 ,每年發(fā)放的電動型汽車牌照數(shù)為構(gòu)成數(shù)列
,每年發(fā)放的電動型汽車牌照數(shù)為構(gòu)成數(shù)列 ,完成下列表格,并寫出這兩個數(shù)列的通項公式;
,完成下列表格,并寫出這兩個數(shù)列的通項公式;
(2)從2013年算起,求二十年發(fā)放的汽車牌照總量.
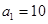 | 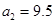 | 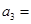 | 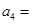 | |
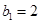 |  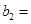 3 3 | 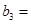 | 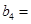 | |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)=log4(4x+1)+kx(k∈R)是偶函數(shù).
(1)求k的值;
(2)設(shè)g(x)=log4 ,若函數(shù)f(x)與g(x)的圖象有且只有一個公共點,求實數(shù)a的取值范圍.
,若函數(shù)f(x)與g(x)的圖象有且只有一個公共點,求實數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com