
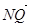 = 2
= 2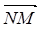 .
.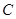 的方程;
的方程;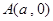 ,點
,點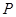 為曲線
為曲線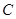 上任一點,求點
上任一點,求點 到點
到點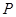 距離的最大值
距離的最大值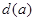 ;
;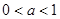 的條件下,設△
的條件下,設△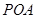 的面積為
的面積為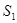 (
(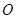 是坐標原點,
是坐標原點,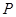 是曲線
是曲線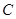 上橫坐標為
上橫坐標為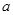 的點),以
的點),以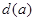 為邊長的正方形的面積為
為邊長的正方形的面積為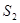 .若正數
.若正數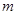 滿足
滿足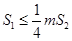 ,問
,問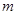 是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
是否存在最小值,若存在,請求出此最小值,若不存在,請說明理由.
 時,
時,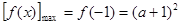 ;
; 時,
時, ;
; 時,,
時,, .所以,
.所以,

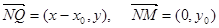
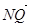 =
=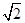
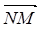
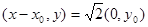
 ∴
∴

 .........................4分
.........................4分 ,則
,則
 ,令
,令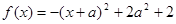 ,
, ,所以,
,所以, ,即
,即 時
時 在
在 上是減函數,
上是減函數,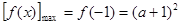 ;
;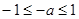 ,即
,即 時,
時, 在
在 上是增函數,在
上是增函數,在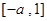 上是減函數,則
上是減函數,則 ;
; ,即
,即 時,
時, 在
在 上是增函數,
上是增函數, .
. . 9分
. 9分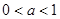 時,
時, ,于是
,于是 ,
, ,
,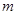 滿足條件,則
滿足條件,則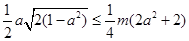 ,即
,即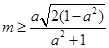 ,
,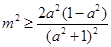 ,令
,令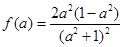 ,設
,設 ,則
,則 ,
,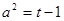 ,于是
,于是 ,
, ,即
,即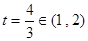 時,
時, ,
, ,
, .所以,
.所以,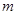 存在最小值
存在最小值 . 14分
. 14分

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com