
已知函數(shù)
(1)當(dāng)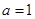 時(shí),求函數(shù)
時(shí),求函數(shù) 在
在 的值域;
的值域;
(2)若關(guān)于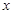 的方程
的方程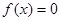 有解,求
有解,求 的取值范圍.
的取值范圍.
(1)值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/51/2/1po4v3.png" style="vertical-align:middle;" /> ;(2) 的取值范圍為
的取值范圍為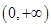 .
.
解析試題分析:(1)當(dāng)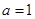 時(shí),
時(shí),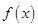 是個(gè)指數(shù)形式的函數(shù),求其值域?yàn)榭梢允褂脫Q元法求解,令
是個(gè)指數(shù)形式的函數(shù),求其值域?yàn)榭梢允褂脫Q元法求解,令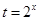 ,將
,將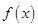 轉(zhuǎn)化為關(guān)于
轉(zhuǎn)化為關(guān)于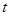 的二次函數(shù)形式,
的二次函數(shù)形式,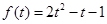 ,根據(jù)二次函數(shù)在給定區(qū)間上求解即可.易錯(cuò)點(diǎn):要注意定義域的變化,其中
,根據(jù)二次函數(shù)在給定區(qū)間上求解即可.易錯(cuò)點(diǎn):要注意定義域的變化,其中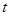 的取值范圍為
的取值范圍為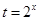 在
在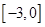 的值域.
的值域.
(2)問(wèn)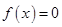 有解,求
有解,求 得取值范圍,可使用分離參數(shù)法,
得取值范圍,可使用分離參數(shù)法,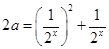 ,保證函數(shù)
,保證函數(shù)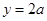 和函數(shù)
和函數(shù)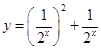 有交點(diǎn)即可,既是求函數(shù)
有交點(diǎn)即可,既是求函數(shù)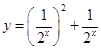 的值域,求值域的方法是先換元后配方,但要注意定義域的變化,求出函數(shù)
的值域,求值域的方法是先換元后配方,但要注意定義域的變化,求出函數(shù)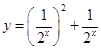 的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/31/1/1l4lj4.png" style="vertical-align:middle;" />,即是
的值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/31/1/1l4lj4.png" style="vertical-align:middle;" />,即是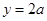 在
在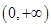 內(nèi),則
內(nèi),則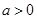 .
.
試題解析:
(1)當(dāng)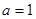 時(shí),
時(shí),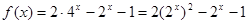 ,令
,令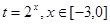 ,則
,則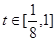 ,因而
,因而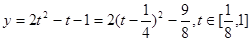 ,故值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/20/d/1fgjs3.png" style="vertical-align:middle;" /> .
,故值域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/20/d/1fgjs3.png" style="vertical-align:middle;" /> .
(2)方法一:由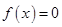 得
得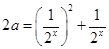 ;由題意可知
;由題意可知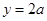 與
與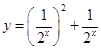 有交點(diǎn)即可.
有交點(diǎn)即可.
令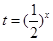 ,得
,得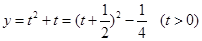 則得
則得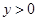 ,所以
,所以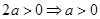 即
即 的取值范圍為
的取值范圍為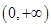 .
.
方法二:方程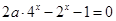 有解,令
有解,令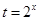 ,則原題意等價(jià)于
,則原題意等價(jià)于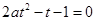 在
在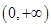 有解,
有解,
記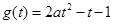 ,當(dāng)
,當(dāng)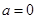 時(shí),得
時(shí),得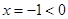 ,不成立;當(dāng)
,不成立;當(dāng)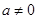 時(shí),根據(jù)根的分布的
時(shí),根據(jù)根的分布的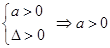 .
.
方法三:方程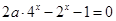 有解,令
有解,令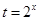 ,則原題意等價(jià)于
,則原題意等價(jià)于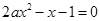 在
在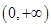 有解,即:
有解,即: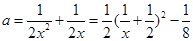 的值域就是
的值域就是 的取值范圍,所以
的取值范圍,所以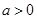 .
.
考點(diǎn):1.值域的求法;2.函數(shù)有解問(wèn)題;3.根的分布.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)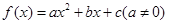 的圖像頂點(diǎn)為
的圖像頂點(diǎn)為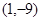 ,且圖像在
,且圖像在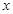 軸截得的線段長(zhǎng)為6.
軸截得的線段長(zhǎng)為6.
(Ⅰ)求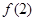 ;
;
(Ⅱ)若 在區(qū)間
在區(qū)間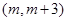 上單調(diào),求
上單調(diào),求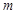 的范圍.
的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知二次函數(shù)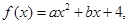 集合
集合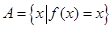
(1)若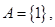 求函數(shù)
求函數(shù) 的解析式;
的解析式;
(2)若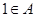 ,且
,且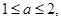 設(shè)
設(shè) 在區(qū)間
在區(qū)間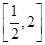 上的最大值、最小值分別為
上的最大值、最小值分別為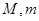 ,記
,記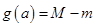 ,求
,求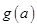 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
集合A是由適合以下性質(zhì)的函數(shù) 構(gòu)成的:對(duì)于定義域內(nèi)任意兩個(gè)不相等的實(shí)數(shù)
構(gòu)成的:對(duì)于定義域內(nèi)任意兩個(gè)不相等的實(shí)數(shù)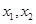 ,都有
,都有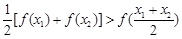 .
.
(1)試判斷 =
=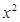 及
及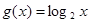 是否在集合A中,并說(shuō)明理由;
是否在集合A中,并說(shuō)明理由;
(2)設(shè) ÎA且定義域?yàn)?0,+¥),值域?yàn)?0,1),
ÎA且定義域?yàn)?0,+¥),值域?yàn)?0,1), ,試寫(xiě)出一個(gè)滿足以上條件的函數(shù)
,試寫(xiě)出一個(gè)滿足以上條件的函數(shù) 的解析式,并給予證明.
的解析式,并給予證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知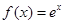 ,
,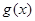 為其反函數(shù).
為其反函數(shù).
(Ⅰ)說(shuō)明函數(shù) 與
與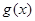 圖象的關(guān)系(只寫(xiě)出結(jié)論即可);
圖象的關(guān)系(只寫(xiě)出結(jié)論即可);
(Ⅱ)證明 的圖象恒在
的圖象恒在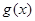 的圖象的上方;
的圖象的上方;
(Ⅲ)設(shè)直線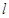 與
與 、
、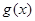 均相切,切點(diǎn)分別為(
均相切,切點(diǎn)分別為(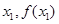 )、(
)、(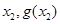 ),且
),且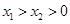 ,求證:
,求證: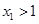 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知函數(shù)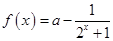 .
.
(1)求證不論 為何實(shí)數(shù),
為何實(shí)數(shù), 總是增函數(shù);
總是增函數(shù);
(2)確定 的值,使
的值,使 為奇函數(shù);
為奇函數(shù);
(3)當(dāng) 為奇函數(shù)時(shí),求
為奇函數(shù)時(shí),求 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知冪函數(shù)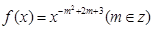 為偶函數(shù),且在區(qū)間
為偶函數(shù),且在區(qū)間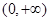 上是單調(diào)增函數(shù)
上是單調(diào)增函數(shù)
(1)求函數(shù) 的解析式;
的解析式;
(2)設(shè)函數(shù)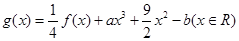 ,其中
,其中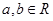 .若函數(shù)
.若函數(shù)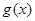 僅在
僅在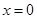 處有極值,求
處有極值,求 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com