
等差數列{an}的公差d不為0,Sn是其前n項和,給出下列命題:
①若d<0,且S3=S8,則S5和S6都是{Sn}中的最大項;
②給定n,對于一切 ,都有
,都有 ;
;
③若d>0,則{Sn}中一定有最小的項;
④存在 ,使
,使 和
和 同號。
同號。
其中正確命題的個數為
A.4 B.3 C.2 D.1
B
【解析】
試題分析:因為{ an }成等差數列,所以其前n項和是關于n的二次函數的形式且缺少常數項。
d<0說明二次函數開口向下,又S3=S8,說明函數關于直線x=5.5對稱,所以S5和S6都是最大項,①正確;
同理,若d>0,說明函數是遞增的,故{Sn}中一定存在最小的項,③正確;
而②是等差中項的推廣,正確;
對于④,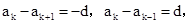 因為d≠0,所以二者異號.
因為d≠0,所以二者異號.
所以正確命題的個數為3個.
故選B。
考點:本題主要考查等差數列的通項公式、求和公式,等差數列的性質。
點評:中檔題,等差數列與一次函數密切相關,特別是其前n項和公式是關于n的二次函數的形式且缺少常數項(d不為0),所以可結合二次函數性質解題。


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| an |
| pn+q |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com