函數(shù)
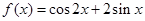
的最小值和最大值分別為( )
試題分析:

,設
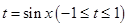
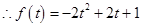
結合二次函數(shù)圖像可知函數(shù)最大值
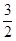
,最小值
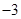
點評:二次函數(shù)當自變量在某一范圍內求其最值時需結合函數(shù)圖象考慮
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知二次函數(shù)
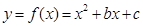
的圖象過點(1,13),圖像關于直線
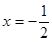
對稱。
(1)求
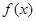
的解析式。
(2)已知
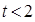
,
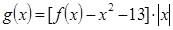
,
① 若函數(shù)
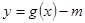
的零點有三個,求實數(shù)
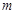
的取值范圍;
②求函數(shù)
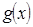
在[
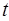
,2]上的最小值。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)f(x)=x2+2ax+3,x∈[-4,6].
(1)當a=-2時,求f(x)的最值;
(2)求實數(shù)a的取值范圍,使y=f(x)在區(qū)間[-4,6]上是單調函數(shù);
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)

的兩個零點分別在區(qū)間

和區(qū)間

內,則實數(shù)
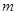
的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本題滿分12分)
已知二次函數(shù)

滿足

且

.
(Ⅰ)求

的解析式;
(Ⅱ)當

時,不等式:

恒成立,求實數(shù)

的范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
對任意的實數(shù)
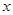
,不等式
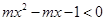
恒成立,則實數(shù)
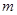
的取值范圍是 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
二次函數(shù)
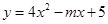
的圖象的對稱軸為
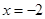
,則當
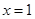
時,
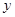
的值為( )
A.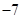 | B.1 | C.17 | D.25 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如果二次函數(shù)
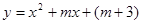
有兩個不同的零點,則
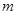
的取值范圍是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
求函數(shù)f(x)="sinx+cosx+sinxcosx." x∈﹝0,
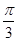
﹞的最大值并求出相應的x值.
查看答案和解析>>

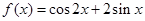 的最小值和最大值分別為( )
的最小值和最大值分別為( )



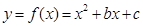 的圖象過點(1,13),圖像關于直線
的圖象過點(1,13),圖像關于直線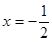 對稱。
對稱。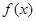 的解析式。
的解析式。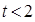 ,
,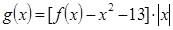 ,
,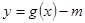 的零點有三個,求實數(shù)
的零點有三個,求實數(shù)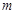 的取值范圍;
的取值范圍;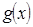 在[
在[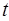 ,2]上的最小值。
,2]上的最小值。