
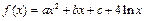 的極值點為
的極值點為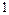 和
和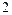 .
.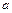 ,
,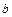 的值;
的值;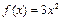 根的個數(shù);
根的個數(shù);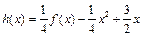 ,斜率為
,斜率為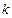 的直線與曲線
的直線與曲線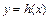 交于
交于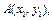
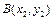
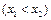 兩點,試比較
兩點,試比較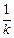 與
與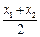 的大小,并給予證明.
的大小,并給予證明.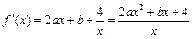 ,
,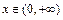 ,……………… 1分
,……………… 1分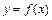 的極值點為
的極值點為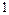 和
和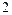 ,
,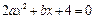 的根為
的根為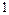 和
和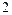 ,
,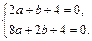 解得
解得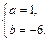 ……………………3分
……………………3分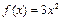 得
得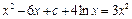 ,
, 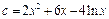 ,設(shè)
,設(shè)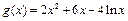 ,
, 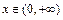 .
.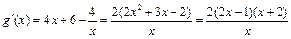 , ………………5分
, ………………5分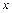 變化時,
變化時,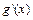 與
與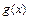 的變化情況如下表:
的變化情況如下表: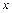 | 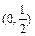 | 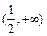 |
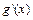 | - | + |
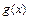 | 單調(diào)遞減 | 單調(diào)遞增 |
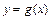 的單調(diào)減區(qū)間為
的單調(diào)減區(qū)間為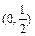 ,單調(diào)增區(qū)間為
,單調(diào)增區(qū)間為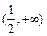 .…6分
.…6分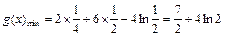 ,
,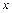 正向趨近于0時,
正向趨近于0時,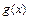 趨近于
趨近于 ,
,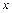 趨近于
趨近于 時,
時,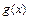 趨近于
趨近于 . ………………7分
. ………………7分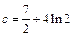 時,方程只有一解;
時,方程只有一解;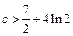 時,方程有兩解;
時,方程有兩解;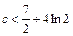 時,方程無解.
時,方程無解.  ………………9分
………………9分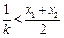 . ……………10分
. ……………10分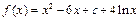 ,
,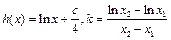 ,
,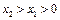 .
.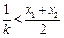 ,即證
,即證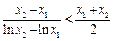 ,
,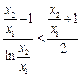 ,(因為
,(因為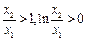 )
)
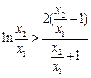 .只需證
.只需證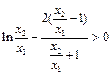 .(*)…………………12分
.(*)…………………12分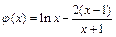
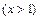 ,
,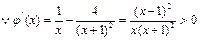 ,
,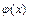 在
在 單調(diào)遞增,
單調(diào)遞增,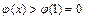 ,
,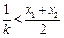 . ………………… 14分
. ………………… 14分

 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.a(chǎn)<b<c | B.c<a<b |
| C.b<a<c | D.b<c<a |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
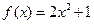 ,值域為
,值域為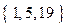 的“孿生函數(shù)”共有______個.
的“孿生函數(shù)”共有______個.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.[2,5] | B.[1,+∞) | C.[2,10] | D.[2,13] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 是正常數(shù),
是正常數(shù), ,
, ,則
,則 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng) 時上式
時上式 (
(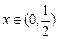 )的最小值為
)的最小值為 .
.查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com