
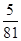 ;(2)分布列詳見解析,
;(2)分布列詳見解析,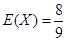 .
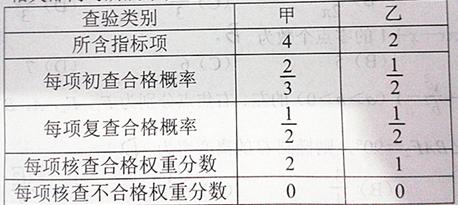
.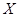 有4種情況:當
有4種情況:當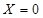 時,表示既沒有獎勵又沒有罰款的情況,也就是第一問的情況;當
時,表示既沒有獎勵又沒有罰款的情況,也就是第一問的情況;當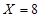 時,表示累計權重分數為9分,也就是甲的4個指標項都合格,而乙中的2個指標項只有1個合格;當
時,表示累計權重分數為9分,也就是甲的4個指標項都合格,而乙中的2個指標項只有1個合格;當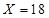 時,表示累計權重分數為10分,也就是說甲乙中的所以指標項都合格的情況;當
時,表示累計權重分數為10分,也就是說甲乙中的所以指標項都合格的情況;當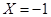 時,表示累計權重分數為7分,也就是甲中的4個指標項有3個合格1個不合格,乙中的2個指標項1個合格1個不合格,利用分析的情況列出概率表達式,列出分布列,利用期望的計算公式求數學期望.
時,表示累計權重分數為7分,也就是甲中的4個指標項有3個合格1個不合格,乙中的2個指標項1個合格1個不合格,利用分析的情況列出概率表達式,列出分布列,利用期望的計算公式求數學期望.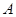 ,“初查階段乙類的一個指標項合格”為事件
,“初查階段乙類的一個指標項合格”為事件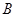 ,“復查階段一個指標項合格”為事件
,“復查階段一個指標項合格”為事件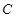 ,則
,則 ,
,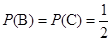 .
. ,則
,則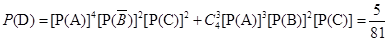 . 4分
. 4分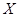 的可能取值為-1,0,8,18.
的可能取值為-1,0,8,18.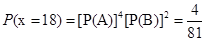 ,
,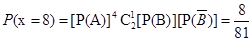 ,
,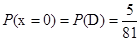 ,
,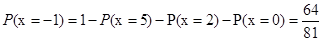 .
.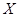 的分布列為
的分布列為| X | -1 | 0 | 8 | 18 | |
| P | 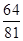 | 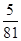 | 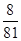 | 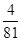 | 10分 |
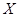 的數學期望
的數學期望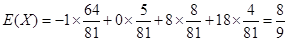 (萬元). 12分
(萬元). 12分

 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案科目:高中數學 來源:不詳 題型:解答題
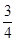 ,
,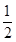 ,
,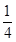 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 魚的 質量 | [1.00, 1.05) | [1.05, 1.10) | [1.10, 1.15) | [1.15, 1.20) | [1.20, 1.25) | [1.25, 1.30) |
| 魚的 條數 | 3 | 20 | 35 | 31 | 9 | 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.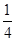 | B. | C.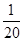 | D.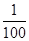 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.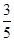 ; ; | B.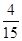 ; ; | C.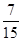 ; ; | D. . . |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com