
已知向量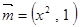 ,
, ,其中
,其中 .函數
.函數 在區間
在區間 上有最大值為4,設
上有最大值為4,設 .
.
(1)求實數 的值;
的值;
(2)若不等式 在
在 上恒成立,求實數
上恒成立,求實數 的取值范圍.
的取值范圍.
 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源:2013-2014學年上海市楊浦區高三上學期學業質量調研理科數學試卷(解析版) 題型:解答題
已知向量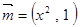 ,
, ,其中
,其中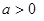 .函數
.函數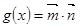 在區間
在區間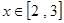 上有最大值為4,設
上有最大值為4,設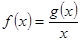 .
.
(1)求實數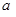 的值;
的值;
(2)若不等式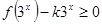 在
在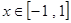 上恒成立,求實數
上恒成立,求實數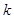 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年浙江省寧波市象山中學(象山港書院)高三(上)期中數學試卷(文科)(解析版) 題型:填空題
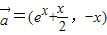 ,
,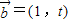 ,若函數
,若函數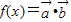 在區間(-1,1)上存在單調遞增區間,則t的取值范圍是 .
在區間(-1,1)上存在單調遞增區間,則t的取值范圍是 .查看答案和解析>>
科目:高中數學 來源: 題型:
已知向量![]() =(
=(![]() ),
),![]() =(
=(![]() ,
,![]()
![]() ),其中(
),其中(![]() ).函數,
).函數,![]() 其圖象的一條對稱軸為
其圖象的一條對稱軸為![]() .
.
(I)求函數![]() 的表達式及單調遞增區間;
的表達式及單調遞增區間;
(Ⅱ)在△ABC中,a、b、c分別為角A、B、C的對邊,S為其面積,若![]() =1,b=l,
=1,b=l,
S△ABC=![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知向量![]() =(
=(![]() ),
),![]() =(
=(![]() ,
,![]()
![]() ),其中(
),其中(![]() ).函數,
).函數,![]() 其圖象的一條對稱軸為
其圖象的一條對稱軸為![]() .
.
(I)求函數![]() 的表達式及單調遞增區間;
的表達式及單調遞增區間;
(Ⅱ)在△ABC中,a、b、c分別為角A、B、C的對邊,S為其面積,若![]() =1,b=l,S△ABC=
=1,b=l,S△ABC=![]() ,求a的值.
,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com