Question

已知函數(shù)為奇函數(shù).

（1）若，求函數(shù)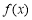的解析式；

（2）當(dāng)時，不等式在上恒成立，求實數(shù)的最小值；

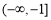（3）當(dāng)時，求證：函數(shù)在上至多有一個零點.

 

Answer 1

（1）；（2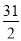） （3）見解析

【解析】

試題分析：（1）由函數(shù)為奇函數(shù),得恒成立,可求的值；

由，從而可得函數(shù)的解析式；

（2）當(dāng)時，可判斷其在區(qū)間上為單調(diào)函數(shù)，最大值為，要使不等式在上恒成立，只要不小于函數(shù)在區(qū)間區(qū)間上的最大值即可；

（3）當(dāng)時，，要證在上至多有一個零點，

只要證在上是單調(diào)函數(shù)即可,對此可用函數(shù)單調(diào)性的定義來解決.

試題解析：解:（1）∵函數(shù)為奇函數(shù)，

∴，即，

∴， 2分

又，

∴

∴函數(shù)的解析式為. 4分

（2），.

∵函數(shù)在均單調(diào)遞增，

∴函數(shù)在單調(diào)遞增， 6分

∴當(dāng)時，． 7分

∵不等式在上恒成立，

∴，

∴實數(shù)的最小值為． 9分

（3）證明：，

設(shè)，

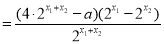11分

∵，

∴

∵，即，

∴，又，

∴，即

∴函數(shù)在單調(diào)遞減， 13分

又，結(jié)合函數(shù)圖像知函數(shù)在上至多有一個零點. 14分

考點：1、函數(shù)的奇偶性；2、函數(shù)的單調(diào)性；3、函數(shù)的最值.