
設數列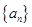 的各項均為正實數,
的各項均為正實數, ,若數列
,若數列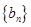 滿足
滿足 ,
,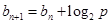 ,其中
,其中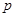 為正常數,且
為正常數,且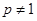 .
.
(1)求數列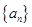 的通項公式;
的通項公式;
(2)是否存在正整數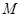 ,使得當
,使得當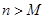 時,
時,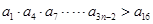 恒成立?若存在,求出使結論成立的
恒成立?若存在,求出使結論成立的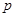 的取值范圍和相應的
的取值范圍和相應的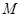 的最小值;若不存在,請說明理由;
的最小值;若不存在,請說明理由;
(3)若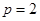 ,設數列
,設數列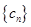 對任意的
對任意的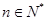 ,都有
,都有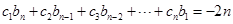 成立,問數列
成立,問數列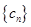 是不是等比數列?若是,請求出其通項公式;若不是,請說明理由.
是不是等比數列?若是,請求出其通項公式;若不是,請說明理由.
(1)詳見解析;(2) ;(3)
;(3)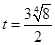 .
.
解析試題分析:(1)由條件可知,數列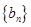 為等差數列,又知
為等差數列,又知 ,其通項公式易求,再根根據數列
,其通項公式易求,再根根據數列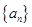 與數列
與數列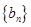 的關系
的關系 ,可求出數列
,可求出數列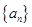 的通項公式;(2)由(1)中所求的數列
的通項公式;(2)由(1)中所求的數列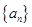 的通項公式,可對
的通項公式,可對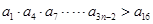 進行化簡,然后再對其考察;(3)當
進行化簡,然后再對其考察;(3)當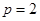 時,結合(1)的結果,可求出
時,結合(1)的結果,可求出 ,代入
,代入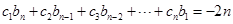 中,設法對其變形處理,找到
中,設法對其變形處理,找到 的遞推關系再進行判斷.
的遞推關系再進行判斷.
試題解析:
(1)因為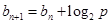 ,所以
,所以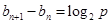 ,所以數列
,所以數列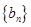 是以
是以 為公差的等差數列,又
為公差的等差數列,又 ,所以
,所以 , 2分
, 2分
故由 ,得
,得 . 4分
. 4分
(2)因為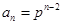 ,所以
,所以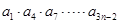

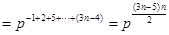 ,
,
又
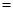
 ,所以
,所以

 , 6分
, 6分
(ⅰ)當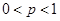 時,
時,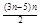
 ,解得
,解得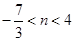 ,不符合題意; 7分
,不符合題意; 7分
(ⅱ)當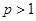 時,
時,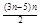
 ,解得
,解得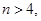 或
或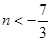 . 8分
. 8分
綜上所述,當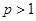 時,存在正整數
時,存在正整數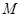 使得
使得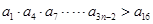 恒成立,且
恒成立,且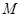 的最小值為4.
的最小值為4.
9分
(3)因為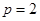 ,由(1)得
,由(1)得 ,
,
所以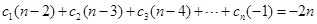 ①,
①,
則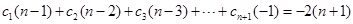 ②,
②,
由② ①,得
①,得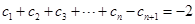 ③, 12分
③, 12分
所以 ④,
④,
再由④ ③,得
③,得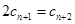 ,即
,即 ,
,
所以當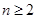 時,數列
時,數列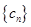 成等比數列, 15分
成等比數列, 15分
又由①式,可得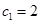 ,
, ,則
,則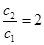 ,所以數列
,所以數列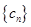 一定是等比數列,且
一定是等比數列,且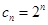 .
.
16分
(說明:若第(3)小題學生由前幾項猜出等比數列,再代回驗證的,扣3分)
考點:等差數列、等比數列.


科目:高中數學 來源: 題型:解答題
已知數列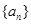 為等差數列,數列
為等差數列,數列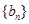 為等比數列,若
為等比數列,若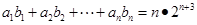 ,且
,且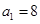 .
.
(1)求數列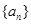 ,
,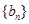 的通項公式;
的通項公式;
(2)是否存在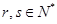 ,使得
,使得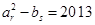 ,若存在,求出所有滿足條件的
,若存在,求出所有滿足條件的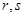 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如果項數均為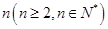 的兩個數列
的兩個數列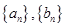 滿足
滿足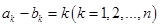 且集合
且集合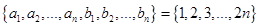 ,則稱數列
,則稱數列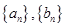 是一對“
是一對“ 項相關數列”.
項相關數列”.
(Ⅰ)設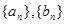 是一對“4項相關數列”,求
是一對“4項相關數列”,求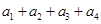 和
和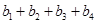 的值,并寫出一對“
的值,并寫出一對“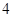 項相
項相
關數列”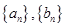 ;
;
(Ⅱ)是否存在“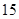 項相關數列”
項相關數列”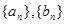 ?若存在,試寫出一對
?若存在,試寫出一對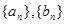 ;若不存在,請說明理由;
;若不存在,請說明理由;
(Ⅲ)對于確定的 ,若存在“
,若存在“ 項相關數列”,試證明符合條件的“
項相關數列”,試證明符合條件的“ 項相關數列”有偶數對.
項相關數列”有偶數對.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
等差數列{an}的前n項和為Sn,已知S3=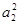 ,且S1,S2,S4成等比數列,
,且S1,S2,S4成等比數列,
(1)求數列{an}的通項公式.
(2)若{an}又是等比數列,令bn=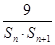 ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com