
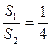 ,推廣到空間可以得到類似結論;已知正四面體P—ABC的內(nèi)切球體積為V1,外接球體積為V2,則
,推廣到空間可以得到類似結論;已知正四面體P—ABC的內(nèi)切球體積為V1,外接球體積為V2,則 ;
; 優(yōu)學名師名題系列答案
優(yōu)學名師名題系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
 滿分12分)
滿分12分)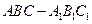 的底面是邊長為2的正三角形,且
的底面是邊長為2的正三角形,且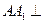 平面
平面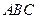 ,
,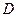 是側棱
是側棱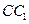 的中點,直線
的中點,直線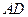 與側面
與側面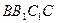 所成的角為45°.
所成的角為45°.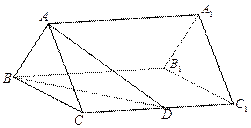
 面角
面角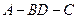 的余弦值;
的余弦值;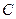 到平面
到平面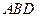 的距離.
的距離.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
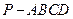 中,底面
中,底面 是邊長為
是邊長為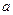 的正方形,
的正方形,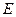 、
、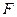 分別為
分別為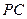 、
、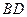 的中點,側面
的中點,側面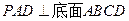 ,且
,且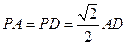 .
.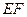 ∥平面
∥平面 ;(2)求三棱錐
;(2)求三棱錐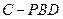 的體積.
的體積. 
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
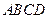 的上底
的上底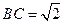 ,
,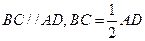 ,
,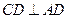 ,平面
,平面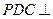 平面
平面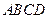 ,
,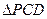 是邊長為
是邊長為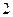 的等邊三角形。
的等邊三角形。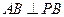 ;
;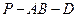 的大小。
的大小。 的體積。
的體積。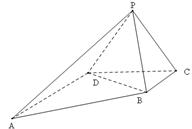
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
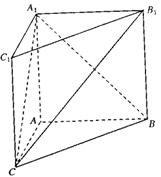
 滿分12分
滿分12分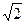 ,BC=
,BC=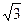 ,AA1=
,AA1=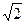 。
。
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
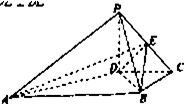
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
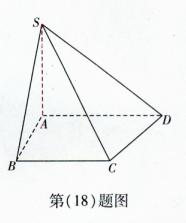
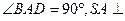 底面ABCD,SA=AB=BC=2,SD與平面ABCD所成角的正切值為
底面ABCD,SA=AB=BC=2,SD與平面ABCD所成角的正切值為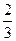 。
。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com