
如圖,在平面直角坐標系xOy中,已知曲線C由圓弧C1和圓弧C2相接而成,兩相接點M,N均在直線x=5上.圓弧C1的圓心是坐標原點O,半徑為13;圓弧C2過點A(29,0).
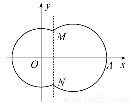
(1)求圓弧C2的方程.
(2)曲線C上是否存在點P,滿足PA=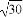 PO?若存在,指出有幾個這樣的點;若不存在,請說明理由.
PO?若存在,指出有幾個這樣的點;若不存在,請說明理由.
(1) (x-14)2+y2=225(5≤x≤29) (2) 不存在,理由見解析
【解析】(1)圓弧C1所在圓的方程為x2+y2=169,令x=5,解得M(5,12),N(5, -12).
則線段AM中垂線的方程為y-6=2(x-17),令y=0,得圓弧C2所在圓的圓心為(14,0),
又圓弧C2所在圓的半徑為r2=29-14=15,所以圓弧C2的方程為(x-14)2+y2=225(5≤x≤29).
(2)假設存在這樣的點P(x,y),
則由PA=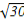 PO,得x2+y2+2x-29=0,
PO,得x2+y2+2x-29=0,
由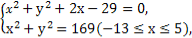
解得x=-70(舍去).
由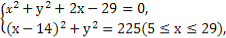
解得x=0(舍去),
綜上知,這樣的點P不存在.
【誤區警示】求圓弧C2的方程時經常遺漏x的取值范圍,其錯誤原因是將圓弧習慣認為或誤認為圓.


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十第八章第一節練習卷(解析版) 題型:解答題
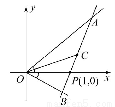
如圖,射線OA,OB分別與x軸正半軸成45°和30°角,過點P(1,0)作直線AB分別交OA,OB于A,B兩點,當AB的中點C恰好落在直線y= x上時,求直線AB的方程.
x上時,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十六第八章第七節練習卷(解析版) 題型:選擇題
若拋物線y2=2px(p>0)的焦點在圓x2+y2+2x-3=0上,則p=( )
(A) (B)1 (C)2 (D)3
(B)1 (C)2 (D)3
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十五第八章第六節練習卷(解析版) 題型:填空題
過雙曲線的右焦點F作實軸所在直線的垂線,交雙曲線于A,B兩點,設雙曲線的左頂點為M,若點M在以AB為直徑的圓的內部,則此雙曲線的離心率e的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十五第八章第六節練習卷(解析版) 題型:選擇題
設雙曲線的一個焦點為F,虛軸的一個端點為B,如果直線FB與該雙曲線的一條漸近線垂直,那么此雙曲線的離心率為( )
(A)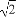 (B)
(B)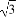 (C)
(C)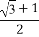 (D)
(D)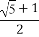
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十二第八章第三節練習卷(解析版) 題型:選擇題
過點A(11,2)作圓x2+y2+2x-4y-164=0的弦,其中弦長為整數的共有( )
(A)16條 (B)17條 (C)32條 (D)34條
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十二第八章第三節練習卷(解析版) 題型:選擇題
圓心在y軸上,半徑為1,且過點(1,2)的圓的方程為( )
(A)x2+(y-2)2=1 (B)x2+(y+2)2=1
(C)(x-1)2+(y-3)2=1 (D)x2+(y-3)2=1
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十三第八章第四節練習卷(解析版) 題型:解答題
過點Q(-2,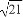 )作圓O:x2+y2=r2(r>0)的切線,切點為D,且|QD|=4.
)作圓O:x2+y2=r2(r>0)的切線,切點為D,且|QD|=4.
(1)求r的值.
(2)設P是圓O上位于第一象限內的任意一點,過點P作圓O的切線l,且l交x軸于點A,交y軸于點B,設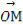 =
=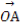 +
+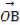 ,求|
,求|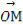 |的最小值(O為坐標原點).
|的最小值(O為坐標原點).
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業五十一第八章第二節練習卷(解析版) 題型:選擇題
對任意實數a,直線y=ax-3a+2所經過的定點是( )
(A)(2,3) (B)(3,2)
(C)(-2,3) (D)(3,-2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com